In the realm of mathematics, fractions are a fundamental concept that helps us understand and manipulate parts of a whole. Among these, improper fractions stand out as a unique and essential component. An improper fraction is a type of fraction where the numerator is greater than or equal to the denominator, resulting in a value greater than one. This article delves into the intricacies of improper fractions, starting with **Understanding the Concept of Improper Fractions**, where we explore the definition, examples, and how they differ from proper fractions. We will then examine **Mathematical Operations with Improper Fractions**, detailing how to perform addition, subtraction, multiplication, and division with these fractions. Finally, we will discuss **Real-World Applications and Practical Uses**, highlighting how improper fractions are utilized in everyday life and various fields such as cooking, engineering, and finance. By grasping these aspects, readers will gain a comprehensive understanding of improper fractions and their significance in mathematical and practical contexts. Let's begin by diving into the foundational concept of what improper fractions are and how they work.

Understanding the Concept of Improper Fractions

Understanding the concept of improper fractions is a fundamental aspect of mathematics, particularly in the realm of fractions. To grasp this concept fully, it is essential to delve into several key areas. First, a clear **Definition and Basic Explanation** of what improper fractions are and how they differ from other types of fractions is crucial. This foundational knowledge sets the stage for further exploration. Next, examining **Visual Representation and Examples** helps to solidify the understanding by providing concrete illustrations and practical scenarios where improper fractions are applied. Finally, **Distinguishing from Proper Fractions** ensures that learners can identify and differentiate between these two types of fractions, which is vital for accurate mathematical operations. By exploring these three facets, individuals can develop a comprehensive understanding of improper fractions. Let's begin by defining and explaining what improper fractions are, laying the groundwork for a deeper exploration of this important mathematical concept.

Definition and Basic Explanation

An improper fraction is a fundamental concept in mathematics that extends the understanding of fractions beyond the conventional mixed numbers. At its core, an improper fraction is a type of fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). This contrasts with proper fractions, where the numerator is always less than the denominator. For instance, 3/2 and 5/3 are examples of improper fractions because in each case, the numerator exceeds or equals the denominator. To grasp this concept fully, it's essential to understand how improper fractions differ from mixed numbers and proper fractions. A mixed number combines a whole number with a proper fraction, such as 2 1/3. In contrast, an improper fraction represents this same value but in a single fraction form; for example, 2 1/3 can be converted into an improper fraction as 7/3. This conversion involves multiplying the whole number by the denominator and then adding the numerator before placing it over the original denominator. Improper fractions are not inherently "improper" in a negative sense; rather, they offer a versatile way to express quantities that are greater than one whole unit. They are particularly useful in various mathematical operations such as addition, subtraction, multiplication, and division of fractions. For example, when adding two mixed numbers like 2 1/3 and 1 2/3, converting them into improper fractions (7/3 and 5/3) simplifies the process significantly. Moreover, improper fractions play a crucial role in algebraic manipulations and solving equations involving rational expressions. They provide a uniform way to handle complex calculations by maintaining consistency in the form of fractions throughout the problem-solving process. Understanding how to convert between mixed numbers and improper fractions is thus a key skill for anyone delving into advanced mathematical concepts. In practical terms, improper fractions can also be seen in real-world applications such as cooking recipes or engineering measurements where precise quantities are essential. For instance, if a recipe calls for 2 3/4 cups of flour but you need to scale it up or down, working with improper fractions like 11/4 cups can streamline your calculations. In summary, improper fractions are an integral part of mathematical literacy that allows for more flexible and efficient handling of numerical values greater than one whole unit. By recognizing their definition and understanding how they differ from other types of fractions, individuals can enhance their problem-solving abilities across various mathematical disciplines and practical scenarios. This foundational knowledge sets the stage for more advanced explorations into algebraic manipulations and rational expressions, making it a vital component of any comprehensive understanding of fractions.

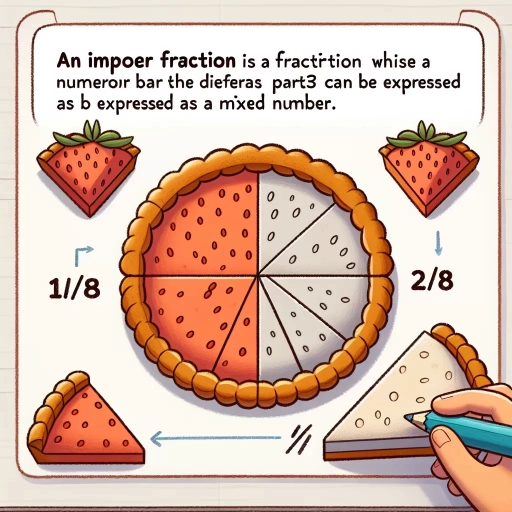
Visual Representation and Examples

Understanding the concept of improper fractions can be significantly enhanced through visual representation, which helps to clarify the relationship between the numerator and the denominator. An improper fraction is defined as a fraction where the numerator is greater than or equal to the denominator. Visualizing these fractions can make them more tangible and easier to comprehend. One effective way to visually represent improper fractions is by using circles or rectangles divided into equal parts. For instance, consider the improper fraction 3/2. You can draw a circle and divide it into two equal parts. Then, shade three of these parts to represent the numerator. This visual aid shows that the fraction exceeds one whole unit, as three parts are shaded out of two possible parts, illustrating why it is considered improper. Another example involves using real-world objects. Imagine you have a pizza that is cut into 4 slices, but you eat 5 slices. This scenario can be represented by the improper fraction 5/4. By drawing a pizza and shading 5 out of 4 slices, you can see that you have consumed more than one whole pizza, making it an improper fraction. Visual representations also help in converting improper fractions to mixed numbers, which can be more intuitive for some learners. For example, take the improper fraction 7/3. You can draw three rows of seven dots each and then group them into sets of three. This will show that there are two complete sets (6 dots) and one additional dot left over. This translates to the mixed number 2 1/3, where 2 represents the whole units and 1/3 represents the remaining part. In addition to these methods, using number lines can further solidify understanding. Plotting improper fractions on a number line allows students to see their position relative to whole numbers and other fractions. For example, plotting 3/2 on a number line shows that it falls between 1 and 2 but closer to 2, reinforcing its improper nature. Moreover, technology can be leveraged to create interactive visual representations. Online tools and apps allow students to manipulate digital shapes and numbers, providing an engaging way to explore improper fractions. These tools often include features like drag-and-drop interfaces and real-time feedback, making learning more dynamic and fun. In conclusion, visual representation is a powerful tool for understanding improper fractions. By using various methods such as divided shapes, real-world objects, mixed numbers, number lines, and interactive technology, learners can gain a deeper insight into how these fractions work. These visual aids not only make the concept more accessible but also foster a stronger connection between abstract mathematical concepts and tangible real-world applications.

Distinguishing from Proper Fractions

When delving into the realm of fractions, it is crucial to distinguish between proper and improper fractions, as each type serves a distinct purpose and has its own set of characteristics. Proper fractions are those where the numerator (the top number) is less than the denominator (the bottom number). For instance, 3/4 is a proper fraction because 3 is less than 4. These fractions represent a part of a whole and are often used to describe portions or percentages. On the other hand, improper fractions have a numerator that is greater than or equal to the denominator. An example of an improper fraction is 5/4, where 5 exceeds 4. Improper fractions can be converted into mixed numbers, which consist of a whole number part and a proper fraction part. For example, 5/4 can be expressed as \(1 \frac{1}{4}\). Understanding the distinction between these two types of fractions is essential for various mathematical operations and real-world applications. In algebra and calculus, improper fractions are frequently used to simplify complex expressions and solve equations. In everyday life, improper fractions can help in measuring quantities that exceed one unit. For instance, if you have 3 1/2 cups of flour, this mixed number represents an improper fraction (7/2) in disguise. Moreover, recognizing whether a fraction is proper or improper aids in performing arithmetic operations such as addition, subtraction, multiplication, and division. When adding or subtracting fractions, ensuring they have common denominators is vital; improper fractions can sometimes complicate this process but also offer flexibility when dealing with mixed numbers. The ability to convert between proper and improper fractions enhances problem-solving skills and provides multiple ways to approach mathematical problems. This versatility is particularly useful in advanced mathematics where fractions are used extensively. For example, in rational expressions and equations, being able to manipulate both proper and improper fractions allows for more efficient simplification and solution-finding processes. In conclusion, distinguishing between proper and improper fractions is fundamental to mastering fraction arithmetic and understanding their applications across various fields. By recognizing the differences and knowing how to convert between these types of fractions, individuals can better navigate mathematical challenges and apply these concepts effectively in real-world scenarios. This foundational knowledge not only strengthens mathematical literacy but also fosters a deeper appreciation for the intricacies of numerical relationships.

Mathematical Operations with Improper Fractions

Mathematical operations involving improper fractions are fundamental to advanced arithmetic and algebra. Understanding how to manipulate these fractions is crucial for solving complex problems in various fields, including science, engineering, and finance. This article delves into three key aspects of working with improper fractions: adding and subtracting, multiplying and dividing, and converting between improper and mixed fractions. Each of these operations requires a distinct set of skills and strategies. When adding and subtracting improper fractions, it is essential to ensure that the denominators are the same, often requiring the use of the least common multiple (LCM). Multiplying and dividing improper fractions involve different rules, with multiplication requiring the multiplication of numerators and denominators separately, while division involves inverting the second fraction and then multiplying. Converting between improper and mixed fractions is also vital, as it allows for the representation of fractions in different forms depending on the context of the problem. By mastering these operations, individuals can enhance their mathematical proficiency and tackle a wide range of problems with confidence. In the following sections, we will explore each of these topics in detail, starting with the basics of adding and subtracting improper fractions. This foundational understanding will provide a solid groundwork for the more complex operations that follow.

Adding and Subtracting Improper Fractions

Adding and subtracting improper fractions is a fundamental skill in mathematics that builds upon the understanding of what improper fractions are. An improper fraction is one where the numerator is greater than the denominator, essentially representing a quantity that is more than one whole. To perform these operations, you must follow specific steps that ensure accuracy and simplicity. ### Adding Improper Fractions When adding improper fractions, the process is similar to adding proper fractions, but with an additional consideration for the whole number part if it exists after simplification. Here are the steps: 1. **Ensure Common Denominators**: The first step is to ensure that both fractions have the same denominator. If they do not, find the least common multiple (LCM) of the denominators and convert each fraction accordingly. 2. **Add Numerators**: Once both fractions have the same denominator, add the numerators together while keeping the denominator unchanged. 3. **Simplify if Necessary**: After adding, simplify the resulting fraction if possible by dividing both the numerator and denominator by their greatest common divisor (GCD). 4. **Convert to Mixed Number (Optional)**: If desired, convert the improper fraction back into a mixed number for better readability. For example, consider adding \( \frac{7}{4} \) and \( \frac{5}{4} \): - Both fractions already have a common denominator of 4. - Add the numerators: \( 7 + 5 = 12 \). - The resulting fraction is \( \frac{12}{4} \), which simplifies to \( 3 \). ### Subtracting Improper Fractions Subtracting improper fractions follows a similar procedure but involves subtracting the numerators instead of adding them: 1. **Ensure Common Denominators**: Ensure both fractions have the same denominator by finding their LCM if necessary. 2. **Subtract Numerators**: Subtract the numerator of the second fraction from the numerator of the first fraction while keeping the denominator unchanged. 3. **Simplify if Necessary**: Simplify the resulting fraction if possible by dividing both the numerator and denominator by their GCD. 4. **Convert to Mixed Number (Optional)**: Convert back to a mixed number if desired for clarity. For instance, consider subtracting \( \frac{9}{6} \) from \( \frac{11}{6} \): - Both fractions already share a common denominator of 6. - Subtract the numerators: \( 11 - 9 = 2 \). - The resulting fraction is \( \frac{2}{6} \), which simplifies to \( \frac{1}{3} \). ### Practical Applications Understanding how to add and subtract improper fractions is crucial in various real-world applications such as cooking, engineering, and finance. For example, in cooking recipes that involve mixing ingredients in fractional quantities, being able to add or subtract these amounts accurately ensures that dishes turn out correctly. In engineering and construction projects, precise calculations involving fractions are essential for accurate measurements and material estimations. In conclusion, adding and subtracting improper fractions involves ensuring common denominators, performing arithmetic operations on numerators while maintaining denominators constant, simplifying results when necessary, and optionally converting back into mixed numbers for clarity. These skills are foundational in mathematical operations involving improper fractions and have practical applications across multiple fields. By mastering these techniques, individuals can enhance their problem-solving abilities in both academic settings and everyday life scenarios involving fractional quantities.

Multiplying and Dividing Improper Fractions

Multiplying and dividing improper fractions are fundamental operations in mathematics that build upon the understanding of improper fractions themselves. An improper fraction is a fraction where the numerator is greater than the denominator, essentially representing a quantity greater than one. When it comes to multiplying improper fractions, the process is straightforward and similar to multiplying proper fractions. You simply multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator. For example, if you want to multiply \( \frac{3}{2} \) by \( \frac{5}{3} \), you would calculate \( 3 \times 5 = 15 \) for the numerator and \( 2 \times 3 = 6 \) for the denominator, resulting in \( \frac{15}{6} \). This can then be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD), which in this case is 3, yielding \( \frac{5}{2} \). Dividing improper fractions involves a slightly different approach but is equally manageable. To divide one improper fraction by another, you invert the second fraction (i.e., flip its numerator and denominator) and then multiply as you would with multiplication. For instance, to divide \( \frac{7}{4} \) by \( \frac{3}{5} \), you would first invert the second fraction to get \( \frac{5}{3} \), then multiply: \( 7 \times 5 = 35 \) for the numerator and \( 4 \times 3 = 12 \) for the denominator, giving you \( \frac{35}{12} \). This result is already in its simplest form. Understanding these operations is crucial because they allow you to perform complex calculations involving mixed numbers and improper fractions seamlessly. For example, if you have a recipe that requires \( 2\frac{1}{3} \) cups of flour but you only have a measuring cup that can handle improper fractions, converting the mixed number to an improper fraction (\( \frac{7}{3} \)) and then performing multiplication or division as needed becomes essential. Moreover, these skills are not limited to simple arithmetic; they are foundational in algebra and higher mathematics where fractions are used extensively. Being able to manipulate improper fractions with ease allows students to tackle more advanced problems with confidence. Additionally, real-world applications such as cooking, engineering, and finance often require precise calculations involving fractions, making proficiency in multiplying and dividing improper fractions a valuable skill. In summary, multiplying and dividing improper fractions are essential mathematical operations that require a clear understanding of fraction manipulation. By following simple rules—multiplying numerators and denominators for multiplication and inverting the divisor for division—you can perform these operations accurately. These skills are not only fundamental in basic arithmetic but also critical in more advanced mathematical disciplines and practical applications. Mastering these operations enhances problem-solving abilities and ensures accuracy in various fields where precision is paramount.

Converting Between Improper and Mixed Fractions

Converting between improper and mixed fractions is a fundamental skill in mathematics, particularly when working with fractions. An improper fraction is one where the numerator is greater than or equal to the denominator, while a mixed fraction combines a whole number with a proper fraction. Understanding how to convert between these two forms enhances flexibility and accuracy in various mathematical operations. To convert an improper fraction to a mixed fraction, you start by dividing the numerator by the denominator. The quotient becomes the whole number part of the mixed fraction, and the remainder becomes the new numerator. For example, consider the improper fraction \( \frac{13}{4} \). Dividing 13 by 4 gives you a quotient of 3 and a remainder of 1. Thus, \( \frac{13}{4} \) converts to \( 3\frac{1}{4} \). This process can be applied universally to any improper fraction. Conversely, converting a mixed fraction to an improper fraction involves multiplying the whole number part by the denominator and then adding the numerator. This sum becomes the new numerator, while the denominator remains unchanged. For instance, take the mixed fraction \( 2\frac{3}{5} \). Multiply 2 by 5 to get 10, then add 3 to get 13. Therefore, \( 2\frac{3}{5} \) converts to \( \frac{13}{5} \). This method ensures that you can seamlessly switch between these forms depending on the context of your calculations. Mastering these conversions is crucial for performing various mathematical operations such as addition, subtraction, multiplication, and division involving fractions. For example, when adding or subtracting fractions with different denominators, converting them into improper fractions can simplify finding common denominators. Similarly, in multiplication and division scenarios involving mixed numbers, converting them into improper fractions can streamline calculations. Moreover, understanding these conversions helps in real-world applications where fractions are used extensively. In cooking recipes, for instance, measurements often involve mixed fractions (e.g., \( 2\frac{1}{2} \) cups), but converting these into improper fractions (e.g., \( \frac{5}{2} \) cups) can facilitate scaling recipes up or down accurately. In conclusion, converting between improper and mixed fractions is an essential mathematical skill that enhances problem-solving abilities across various contexts. By mastering this technique, individuals can perform complex fraction operations with ease and apply mathematical concepts more effectively in everyday life. Whether you are solving algebraic equations or measuring ingredients for a recipe, being proficient in converting between improper and mixed fractions will undoubtedly prove invaluable.

Real-World Applications and Practical Uses

In today's world, the real-world applications and practical uses of mathematical concepts are multifaceted and indispensable. From the mundane tasks of everyday life to the complex problem-solving in various disciplines, mathematics plays a pivotal role. This article delves into three key areas where mathematics is not just a theoretical construct but a vital tool: Measurement and Quantities in Everyday Life, Problem-Solving in Various Disciplines, and Importance in Advanced Mathematical Concepts. In our daily routines, we often overlook the significance of measurement and quantities, yet they are essential for tasks such as cooking, shopping, and even managing personal finances. Mathematics also serves as a cornerstone for problem-solving across diverse fields like engineering, economics, and medicine, where precise calculations and logical reasoning are crucial. Furthermore, advanced mathematical concepts form the foundation for groundbreaking research and innovations in fields such as physics, computer science, and data analytics. Understanding these applications not only highlights the relevance of mathematics but also underscores its importance in enhancing our quality of life and driving technological advancements. Let us begin by exploring how measurement and quantities permeate our everyday lives, illustrating how these fundamental concepts shape our interactions with the world around us.

Measurement and Quantities in Everyday Life

Measurement and quantities are integral components of everyday life, influencing various aspects of our daily routines and decision-making processes. From the simplest tasks to complex operations, understanding and applying measurements accurately is crucial for efficiency, safety, and precision. For instance, in cooking, measuring ingredients using units such as grams, milliliters, or teaspoons ensures that recipes are followed correctly, resulting in consistent flavors and textures. This attention to detail is equally important in healthcare where dosages of medications must be measured precisely to avoid adverse reactions or inefficacy. In the realm of finance, quantities play a significant role in budgeting and financial planning. Individuals must measure their income against expenses to maintain financial stability, often using fractions or decimals to calculate percentages and ratios. For example, understanding that a 25% discount on a purchase translates to saving one-fourth of the original price helps consumers make informed decisions about their spending. In construction and engineering, accurate measurements are critical for ensuring structural integrity and compliance with building codes. Architects and engineers use precise quantities to design buildings, bridges, and other infrastructure projects, where even minor miscalculations could have catastrophic consequences. Similarly, in science and technology, researchers rely heavily on accurate measurements to conduct experiments and gather data that can lead to groundbreaking discoveries. Moreover, measurement skills are essential in transportation. Pilots must measure fuel consumption, altitude, and airspeed to ensure safe flight operations. Drivers use speedometers to gauge their velocity relative to speed limits, while GPS systems provide precise distance measurements to navigate through unfamiliar territories. Even in sports and fitness, measuring performance metrics such as distance run, calories burned, or heart rate helps athletes optimize their training regimens. Coaches use these measurements to tailor workouts that improve performance without risking injury. In education, teaching children about measurement concepts from an early age lays the foundation for future mathematical understanding. Simple activities like measuring lengths using rulers or counting blocks introduce fundamental principles that later expand into more complex mathematical operations. In conclusion, measurement and quantities permeate every facet of daily life—from mundane tasks like cooking and budgeting to high-stakes activities like engineering and healthcare. The ability to accurately measure and understand quantities is not just a practical skill but a fundamental necessity for achieving precision, safety, and success across various domains. This underscores the importance of mastering measurement concepts early on and applying them effectively in real-world scenarios.

Problem-Solving in Various Disciplines

Problem-solving is a ubiquitous skill that transcends disciplinary boundaries, playing a crucial role in various fields such as mathematics, science, engineering, economics, and even social sciences. In mathematics, problem-solving is fundamental to understanding and applying concepts like improper fractions. For instance, converting an improper fraction to a mixed number or vice versa requires logical reasoning and step-by-step analysis. This skill is not limited to academic exercises; it has real-world applications in fields like finance where improper fractions can represent interest rates or investment returns. In science, problem-solving involves designing experiments, interpreting data, and drawing conclusions—skills that are essential for breakthroughs in fields such as medicine and environmental science. Engineers rely heavily on problem-solving to design efficient systems, troubleshoot issues, and optimize performance. In economics, policymakers use problem-solving to analyze economic data, predict trends, and make informed decisions that impact national policies. Even in social sciences, researchers employ problem-solving techniques to understand human behavior, analyze social phenomena, and develop strategies for social change. The ability to approach problems systematically—identifying the issue, gathering information, formulating solutions, and evaluating outcomes—is a common thread across these disciplines. This versatility underscores the importance of cultivating robust problem-solving skills from an early age, as they are indispensable for tackling complex challenges in both personal and professional contexts. By integrating problem-solving into various disciplines, individuals can develop a holistic understanding of how different fields intersect and influence one another, leading to more innovative and effective solutions in real-world applications.

Importance in Advanced Mathematical Concepts

Advanced mathematical concepts are pivotal in driving innovation and solving complex problems across various real-world applications. These sophisticated ideas, often rooted in abstract algebra, differential equations, and number theory, provide the foundational tools necessary for breakthroughs in science, technology, engineering, and mathematics (STEM) fields. For instance, differential equations are crucial in modeling population dynamics, predicting weather patterns, and understanding the spread of diseases. In engineering, advanced mathematical concepts such as calculus and linear algebra are essential for designing efficient systems, optimizing processes, and ensuring structural integrity. In finance, stochastic processes and probability theory help in risk management and portfolio optimization. Moreover, advanced mathematical concepts underpin many modern technologies, including cryptography for secure data transmission and machine learning algorithms that power artificial intelligence. These concepts also enable scientists to analyze large datasets, make accurate predictions, and uncover hidden patterns in fields like astronomy and genetics. The practical uses of advanced mathematics are evident in everyday life, from GPS navigation systems that rely on geometric calculations to medical imaging techniques like MRI and CT scans that utilize Fourier transforms. By mastering these advanced mathematical concepts, professionals can tackle intricate challenges with precision and creativity, leading to significant advancements in their respective fields. Thus, the importance of advanced mathematical concepts lies not only in their theoretical elegance but also in their profound impact on real-world applications and practical uses.