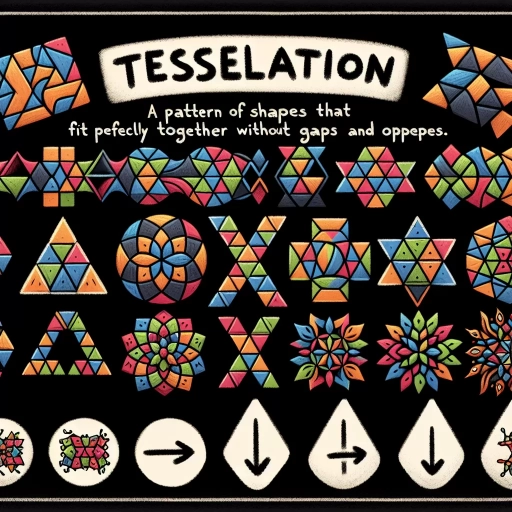
Tessellations are intricate patterns that cover a surface without overlapping or leaving gaps, creating a seamless and visually appealing design. These geometric arrangements have fascinated artists, mathematicians, and scientists for centuries due to their beauty and practical applications. In this article, we will delve into the world of tessellations, starting with the fundamental question: **What is a Tessellation?** This section will explore the basic principles and definitions that underpin these patterns. We will then examine **Types of Tessellations**, highlighting the various forms they can take, from regular and semi-regular to more complex and irregular designs. Finally, we will discuss **Applications and Examples of Tessellations**, showcasing how these patterns are used in art, architecture, science, and everyday life. By understanding what tessellations are, their different types, and their diverse applications, readers will gain a comprehensive appreciation for the significance and versatility of these geometric wonders. Let's begin by answering the core question: **What is a Tessellation?**

What is a Tessellation?

A tessellation is a fascinating concept that has captivated artists, mathematicians, and scientists for centuries. At its core, a tessellation is a repeating pattern of shapes that fit together without overlapping, creating a seamless and often visually striking design. To fully understand the intricacies of tessellations, it is essential to delve into three key areas: **Definition and Basic Concepts**, **Historical Background and Cultural Significance**, and **Mathematical Principles and Geometry**. Starting with the **Definition and Basic Concepts**, we explore the fundamental elements that define a tessellation. This includes understanding the types of shapes that can be used, such as polygons, and how they are arranged to cover a surface completely. By grasping these basics, we lay the groundwork for appreciating the broader implications and applications of tessellations. Beyond the technical aspects, **Historical Background and Cultural Significance** reveal how tessellations have been integral to various cultures and historical periods. From ancient Islamic art to modern-day architecture, tessellations have played a significant role in aesthetics and symbolism. Finally, **Mathematical Principles and Geometry** uncover the underlying mathematical structures that govern tessellations. This involves exploring concepts like symmetry, periodicity, and the geometric properties of the shapes involved. By examining these principles, we can appreciate the beauty and complexity of tessellations from a mathematical perspective. Understanding these three facets provides a comprehensive view of what a tessellation is and why it remains an enduring subject of interest across multiple disciplines. Let us begin by exploring the **Definition and Basic Concepts** that underpin this captivating topic.

Definition and Basic Concepts

A tessellation is a fundamental concept in geometry and art, defined as the covering of a plane with non-overlapping shapes, known as tiles or tesserae, without any gaps or overlaps. This intricate arrangement of shapes can be composed of various geometric figures such as triangles, squares, hexagons, and even more complex polygons. The basic concept of tessellations hinges on the idea that these shapes fit together perfectly to form a larger pattern that extends infinitely in all directions. At its core, a tessellation must adhere to several key principles. First, the tiles must be identical in shape and size to ensure uniformity across the pattern. Second, these tiles must cover the entire plane without any overlaps or gaps, creating a seamless and continuous design. Third, the arrangement of tiles should be such that it can be repeated indefinitely in all directions, forming an infinite pattern. Tessellations can be classified into different types based on the shapes used and their symmetry properties. Regular tessellations are formed by regular polygons where each vertex is surrounded by the same arrangement of polygons. For example, a grid of squares or a honeycomb pattern made of hexagons are classic examples of regular tessellations. Semi-regular tessellations involve a combination of different regular polygons arranged in a specific pattern around each vertex. Irregular tessellations, on the other hand, use irregular shapes and do not follow any specific symmetry rules. The study of tessellations has far-reaching implications across various fields including mathematics, art, architecture, and even biology. In mathematics, tessellations help in understanding geometric transformations and symmetries. In art and design, they provide a rich source of inspiration for creating visually appealing patterns and designs. Architects use tessellations to design efficient and aesthetically pleasing layouts for buildings and public spaces. In biology, natural forms like the arrangement of cells in honeycombs or the structure of certain minerals exhibit tessellations. Historically, tessellations have been a part of human culture for thousands of years. Ancient civilizations such as the Greeks and Romans used mosaic tiles to create intricate floor designs that were essentially tessellations. Islamic art is renowned for its use of geometric patterns that often involve complex tessellations. The Dutch artist M.C. Escher popularized tessellations in modern art through his innovative and imaginative use of interlocking shapes to create mesmerizing patterns. In conclusion, tessellations represent a fascinating intersection of geometry, art, and nature. Their definition and basic concepts provide a foundation for understanding how shapes can be arranged to cover a plane infinitely without gaps or overlaps. Whether in mathematics, art, architecture, or natural forms, tessellations offer a wealth of creative possibilities and practical applications that continue to inspire and intrigue people around the world.

Historical Background and Cultural Significance

Tessellations, the art of covering a surface with non-overlapping shapes, have a rich historical background and profound cultural significance that span across various civilizations and epochs. The earliest known examples of tessellations date back to ancient Mesopotamia, where artisans used glazed tiles to create intricate patterns on walls and floors around 2000 BCE. These early tessellations not only served as decorative elements but also symbolized the cultural and religious beliefs of the time, often depicting mythological creatures and divine figures. In ancient Greece and Rome, tessellations were used extensively in mosaics, which adorned public spaces, temples, and private homes. These mosaics were more than just aesthetic additions; they told stories, commemorated events, and reflected the societal values of the time. The Romans, in particular, perfected the art of mosaic tessellations, creating elaborate designs that showcased their technical skill and artistic flair. The Islamic world also made significant contributions to the art of tessellations. From the 8th century onwards, Islamic artisans developed a unique style of geometric tessellations that adorned mosques, palaces, and other architectural marvels. These intricate patterns, often featuring interlocking polygons and arabesques, were not only visually stunning but also carried deep spiritual meaning. They represented the infinite and the divine, reflecting Islamic beliefs about the unity and complexity of God's creation. In the 20th century, the Dutch artist M.C. Escher revolutionized the concept of tessellations with his innovative and imaginative designs. Escher's work transformed tessellations from a traditional craft into a modern art form, exploring new shapes, symmetries, and themes that captivated audiences worldwide. His contributions not only expanded the artistic possibilities of tessellations but also introduced them to a broader audience, making them a staple of modern art and design. Beyond their aesthetic appeal, tessellations hold significant cultural and mathematical importance. They embody principles of symmetry, geometry, and spatial reasoning, making them a valuable tool in education and scientific inquiry. In many cultures, tessellations are also imbued with symbolic meanings, representing unity, harmony, and the interconnectedness of all things. For instance, in some African cultures, tessellations are used in textiles and pottery to convey messages about community and cooperation. In contemporary times, tessellations continue to inspire artists, designers, and scientists alike. They are used in architecture to create visually striking facades and interiors; in fashion to design unique patterns; and in science to model complex systems and structures. The cultural significance of tessellations lies in their ability to bridge different disciplines and cultures, offering a universal language that transcends time and space. Whether as ancient mosaics or modern digital art, tessellations remain a testament to human creativity and ingenuity, reflecting our enduring fascination with pattern, symmetry, and beauty.

Mathematical Principles and Geometry

Mathematical principles and geometry form the foundational backbone of understanding tessellations. A tessellation, by definition, is a repeating pattern of shapes that fit together without overlapping, covering a flat plane completely. The mathematical underpinnings of tessellations are rooted in geometric concepts such as symmetry, congruence, and regular polygons. Symmetry plays a crucial role as it dictates how the shapes can be arranged to maintain uniformity across the plane. For instance, translational symmetry ensures that the pattern repeats in a linear fashion, while rotational symmetry allows for the rotation of shapes around a central point without disrupting the overall pattern. Geometric shapes, particularly regular polygons like triangles, squares, and hexagons, are commonly used in tessellations due to their ability to tile the plane seamlessly. The properties of these polygons, such as their internal angles and side lengths, are critical in determining whether they can form a tessellation. For example, the internal angle of a regular hexagon is 120 degrees, which allows it to fit perfectly with six other hexagons around a central point, creating a honeycomb-like pattern. This geometric compatibility is essential for creating visually appealing and mathematically sound tessellations. Moreover, the concept of congruence is vital as it ensures that each shape in the tessellation is identical in size and shape to its neighboring shapes. This congruence maintains the integrity of the pattern, preventing any gaps or overlaps that would disrupt the tessellation. Additionally, mathematical principles like Euler's formula for polyhedra can be extended to understand the topological properties of more complex tessellations, especially those involving non-regular polygons or mixed shapes. The study of tessellations also delves into the realm of fractals and self-similarity, where smaller versions of the same shape are used to create larger patterns. This self-similarity is a hallmark of fractal geometry and can lead to intricate and aesthetically pleasing designs. The mathematical rigor behind these patterns allows for their application in various fields such as architecture, art, and even computer graphics. In conclusion, the intersection of mathematical principles and geometry is what makes tessellations possible and fascinating. By understanding the geometric properties of shapes and how they interact through symmetry and congruence, we can create complex yet harmonious patterns that cover the plane without gaps or overlaps. This blend of mathematics and geometry not only enriches our understanding of spatial relationships but also inspires creative expressions across diverse disciplines.

Types of Tessellations

Tessellations, the art of covering a surface with repeating patterns of shapes without overlaps or gaps, have fascinated mathematicians and artists for centuries. This intricate field is divided into three primary categories: Regular Tessellations, Semi-Regular Tessellations, and Irregular Tessellations. Each type offers unique characteristics and applications, making them essential for understanding the broader concept of tessellations. Regular Tessellations, characterized by their uniformity and symmetry, are the most straightforward and aesthetically pleasing. Semi-Regular Tessellations, while less uniform, still maintain a level of order and are often seen in nature and architecture. Irregular Tessellations, on the other hand, break free from traditional symmetry, offering endless possibilities for creative expression. By exploring these three types, we can delve into the mathematical principles and artistic inspirations behind tessellations. Let's begin by examining the foundational aspect of these patterns: Regular Tessellations.

Regular Tessellations

**Regular Tessellations** Regular tessellations are a fundamental and visually striking type of tessellation, characterized by their uniformity and symmetry. These tessellations are composed entirely of regular polygons, where each vertex is identical and surrounded by the same arrangement of polygons. The most common regular tessellations are those made up of equilateral triangles, squares, and hexagons. When we consider the properties of regular polygons, it becomes clear why these three shapes are uniquely suited for forming regular tessellations. An equilateral triangle has an internal angle of 60 degrees, a square has an internal angle of 90 degrees, and a regular hexagon has an internal angle of 120 degrees. These angles allow these polygons to fit together seamlessly without any gaps or overlaps, covering the entire plane perfectly. The equilateral triangle tessellation is one of the simplest and most elegant forms, where each triangle shares edges with six neighboring triangles. This arrangement creates a pattern that is both visually appealing and mathematically intriguing due to its high degree of symmetry. Similarly, the square tessellation forms a grid-like pattern where each square shares edges with four neighboring squares, making it a common motif in architecture and design. The hexagonal tessellation, often referred to as the "honeycomb" pattern due to its resemblance to the structure of honeycombs in beehives, is particularly noteworthy. Each hexagon is surrounded by six other hexagons, creating a highly efficient and stable arrangement that minimizes the perimeter while maximizing the area covered. This property makes hexagonal tessellations appear frequently in nature and engineering applications. Regular tessellations have numerous practical applications across various fields. In architecture, they are used in flooring patterns and wall designs to create aesthetically pleasing and symmetrical layouts. In engineering, the efficiency of hexagonal arrangements makes them ideal for structures such as bridges and aircraft components where strength and stability are crucial. Additionally, regular tessellations play a significant role in art and design, providing artists with a rich source of inspiration for creating intricate and beautiful patterns. From a mathematical perspective, regular tessellations offer insights into geometric properties and symmetries. They are closely related to the concept of wallpaper groups, which classify the different types of symmetries that can be applied to a two-dimensional pattern. Studying regular tessellations helps mathematicians understand deeper principles about space-filling patterns and the inherent beauty of geometric structures. In conclusion, regular tessellations represent a unique blend of mathematical precision and aesthetic appeal. Their ability to cover the plane uniformly with identical regular polygons makes them both fascinating subjects for study and practical tools for various applications. Whether in nature, art, architecture, or engineering, regular tessellations stand as a testament to the harmony between geometry and design.

Semi-Regular Tessellations

Semi-regular tessellations represent a fascinating subset within the broader realm of tessellations, offering a unique blend of symmetry and complexity. Unlike regular tessellations, which are composed of identical regular polygons arranged in a repeating pattern, semi-regular tessellations incorporate multiple types of regular polygons. This diversity introduces an intriguing layer of visual interest and mathematical richness. To qualify as semi-regular, a tessellation must meet specific criteria: it must be composed of regular polygons, each vertex must be surrounded by the same sequence of polygons, and no two adjacent polygons can be the same type. There are exactly eight semi-regular tessellations known, each characterized by its unique combination of polygons and vertex configurations. For instance, the "snub square tiling" features squares and equilateral triangles arranged in a particular sequence around each vertex, while the "rhombitrihexagonal tiling" combines rhombi and hexagons. The study of semi-regular tessellations has deep roots in geometry and has been explored by mathematicians for centuries. These patterns are not only aesthetically pleasing but also hold significant mathematical properties. They exhibit a form of symmetry known as "translational symmetry," meaning that the pattern can be translated (moved) in such a way that it looks the same. This symmetry is crucial in various fields, including architecture, design, and even materials science. In architecture, semi-regular tessellations have inspired the design of intricate mosaics and tilework found in historical buildings around the world. For example, Islamic art is renowned for its use of geometric patterns, including semi-regular tessellations, which adorn mosques and palaces with intricate beauty. These patterns not only add visual appeal but also reflect the cultural and mathematical sophistication of their creators. Beyond aesthetics, semi-regular tessellations have practical applications. In materials science, researchers study these patterns to understand how different shapes can be arranged to achieve optimal structural properties. For instance, certain arrangements of polygons can provide exceptional strength-to-weight ratios, making them ideal for engineering applications such as lightweight yet robust materials. In conclusion, semi-regular tessellations stand as a testament to the beauty and complexity inherent in geometric patterns. Their unique combinations of regular polygons offer a rich field of study that spans from pure mathematics to practical applications. Whether admired for their visual elegance or explored for their mathematical properties, semi-regular tessellations continue to captivate both scholars and enthusiasts alike, highlighting the profound interplay between art and science.

Irregular Tessellations

**Irregular Tessellations** Irregular tessellations represent a fascinating and complex subset of tessellations, deviating from the symmetry and regularity seen in their more structured counterparts. Unlike regular tessellations, which are composed of identical, regular polygons arranged in a repeating pattern, irregular tessellations are formed by non-regular polygons. These polygons can vary in shape and size, yet they still cover the plane without overlapping or leaving gaps. The beauty of irregular tessellations lies in their ability to create visually intriguing patterns that can mimic natural forms or artistic expressions. One of the key characteristics of irregular tessellations is their lack of translational symmetry, meaning that the pattern does not repeat in a straightforward manner. Instead, these tessellations often exhibit more complex symmetries, such as glide reflections or rotational symmetries, which add to their aesthetic appeal. For instance, an irregular tessellation might feature a combination of triangles, quadrilaterals, and hexagons arranged in such a way that each shape fits snugly against its neighbors, creating a mosaic-like effect. Artists and designers frequently exploit the versatility of irregular tessellations to create unique and captivating designs. In architecture, for example, irregular tessellations can be used to design intricate floor patterns or wall coverings that add visual interest to a space. Similarly, in graphic design, these tessellations can be employed to create dynamic backgrounds or textures that stand out from more conventional patterns. From a mathematical perspective, irregular tessellations offer a rich field of study. Mathematicians explore the properties and constraints of these tessellations, such as the types of polygons that can be used and the conditions under which they can tile the plane. This area of study intersects with geometry and combinatorics, providing insights into the fundamental principles that govern spatial arrangements. In nature, irregular tessellations can be observed in the patterns found on butterfly wings, the arrangement of leaves on stems, and even the structure of some crystals. These natural examples highlight the intrinsic beauty and functionality of irregular tessellations, where complexity and variability lead to robust and efficient designs. In conclusion, irregular tessellations embody the creative potential and mathematical depth of tessellations. They challenge traditional notions of symmetry and order while offering a wide range of applications in art, design, and science. Whether used to adorn a building facade or to model natural phenomena, irregular tessellations showcase the versatility and beauty inherent in the art of tiling the plane.

Applications and Examples of Tessellations

Tessellations, the repeating patterns of shapes that fit together without overlapping, have far-reaching applications across various disciplines. These intricate designs not only captivate our aesthetic senses but also serve as fundamental elements in science, technology, nature, and architecture. In the realm of **Art and Design**, tessellations inspire artists to create visually stunning and mathematically precise works. From the intricate mosaics of Islamic art to the geometric patterns in modern graphic design, tessellations add a layer of complexity and beauty that engages viewers on multiple levels. Beyond aesthetics, **Science and Technology** leverage tessellations in fields such as materials science and computer graphics, where they help in understanding and visualizing complex structures. Additionally, **Nature and Architecture** showcase tessellations in the natural world, from the arrangement of leaves on stems to the structural integrity of buildings and bridges. By exploring these diverse applications, we can appreciate the versatility and significance of tessellations in enhancing our understanding and appreciation of the world around us. Let us begin by delving into how tessellations influence **Art and Design**.

Art and Design

In the realm of art and design, tessellations play a pivotal role in creating visually striking and mathematically precise compositions. A tessellation, by definition, is a repeating pattern of shapes that fit together without overlapping, leaving no gaps. This concept has been a cornerstone in various artistic and design disciplines for centuries, offering endless possibilities for creativity and innovation. One of the most celebrated examples of tessellations in art can be found in the works of M.C. Escher, a Dutch artist renowned for his intricate and imaginative designs. Escher's use of tessellations not only showcased his mastery over geometric patterns but also delved into the realm of surrealism, blending mathematics with art in a way that continues to inspire artists today. His famous "Day and Night" print, for instance, features a seamless transition from day to night through a tessellation of birds and fish, highlighting the versatility and aesthetic appeal of these patterns. In design, tessellations are equally influential. They are frequently used in architecture to create visually appealing and structurally sound designs. Islamic art, for example, is replete with intricate tessellations that adorn mosques, palaces, and other architectural marvels. These patterns not only add beauty but also symbolize the infinite and the divine, reflecting the cultural and spiritual significance of the art form. Tessellations also find practical applications in graphic design and textile art. In graphic design, they can be used to create dynamic backgrounds, logos, and other visual elements that capture attention and convey messages effectively. For instance, a company might use a tessellation pattern in its branding to convey unity, continuity, and precision. In textile art, tessellations can be woven into fabrics to produce unique and captivating designs that are both functional and decorative. Moreover, modern technology has expanded the scope of tessellations in art and design. Computer-aided design (CAD) software allows artists and designers to create complex tessellations with ease, enabling them to experiment with various shapes, colors, and patterns. This has led to innovative applications in fields such as urban planning, where tessellations can be used to optimize space usage in urban environments. The educational sector also benefits from the integration of tessellations into art and design curricula. Teaching students about tessellations helps them understand fundamental concepts in geometry and spatial reasoning while fostering creativity and problem-solving skills. This interdisciplinary approach bridges the gap between mathematics and art, making learning more engaging and holistic. In conclusion, tessellations are a powerful tool in the world of art and design, offering a blend of mathematical precision and aesthetic appeal. From the historical masterpieces of M.C. Escher to contemporary applications in architecture, graphic design, and textile art, tessellations continue to inspire creativity and innovation across various disciplines. Their ability to combine beauty with functionality makes them an indispensable element in the creative process, ensuring their relevance and importance for generations to come.

Science and Technology

In the realm of science and technology, tessellations play a pivotal role in various applications, showcasing their versatility and significance. A tessellation, by definition, is a repeating pattern of shapes that fit together without overlapping, and its principles are deeply intertwined with modern technological advancements. One of the most compelling examples is in computer graphics and game development. Here, tessellations are used to create detailed textures and landscapes efficiently. By dividing complex surfaces into simpler, repeating patterns, developers can achieve high-resolution graphics while minimizing computational resources. This technique is particularly evident in games that feature expansive, detailed environments, where the seamless integration of tessellations ensures smooth gameplay and realistic visuals. Another significant application lies in architecture and urban planning. Tessellations are used to design efficient and aesthetically pleasing structures. For instance, the use of hexagonal tiles in flooring and roofing systems maximizes space while providing structural integrity. This geometric approach also influences the design of cities, where tessellations help in planning grid systems that optimize land use and facilitate efficient transportation networks. Additionally, in materials science, tessellations are crucial for understanding and creating advanced materials such as graphene and other nanomaterials. The hexagonal structure of graphene, for example, is a perfect tessellation that contributes to its exceptional strength and conductivity. In engineering, tessellations are vital for the design of composite materials and structures. By arranging different materials in a tessellated pattern, engineers can create lightweight yet robust components for aerospace and automotive industries. This approach also extends to biomedical engineering, where tessellations are used in the design of prosthetics and implants. The repeating patterns help in achieving uniform stress distribution and enhancing the durability of these medical devices. Furthermore, in data visualization and geographic information systems (GIS), tessellations are instrumental in representing complex data sets. Techniques like Voronoi diagrams and Delaunay triangulations are forms of tessellations that help in partitioning space based on proximity to points in a specific subset of the plane. These methods are essential for analyzing spatial data, such as population density, climate patterns, and resource distribution, making them invaluable tools for researchers and policymakers. Lastly, the artistic and educational aspects of tessellations should not be overlooked. In mathematics education, tessellations serve as an engaging tool to teach geometric concepts and spatial reasoning. They also inspire artistic creations, from traditional Islamic art to modern digital art, where the symmetry and beauty of tessellations are celebrated. This intersection of art and science underscores the universal appeal and practical utility of tessellations across diverse fields. In summary, the applications and examples of tessellations in science and technology are myriad and impactful. From enhancing computer graphics to designing advanced materials, and from urban planning to data visualization, tessellations demonstrate their profound influence on modern technological advancements. Their ability to optimize space, enhance efficiency, and inspire creativity makes them an indispensable element in various scientific and technological endeavors.

Nature and Architecture

Nature and architecture have long been intertwined, with each influencing the other in profound ways. The intricate patterns and structures found in nature have inspired some of the most iconic architectural designs throughout history. Tessellations, in particular, play a significant role in this symbiotic relationship. A tessellation is a repeating pattern of shapes that fit together without overlapping, and it can be observed in various natural forms such as the hexagonal cells of honeycombs, the scales of fish, and the branching patterns of trees. Architects have often drawn upon these natural tessellations to create aesthetically pleasing and functionally efficient designs. For instance, the ancient Greeks used tessellations in their mosaics to adorn public spaces and private homes, while Islamic architecture is renowned for its intricate geometric patterns that cover walls, ceilings, and floors. These designs not only add beauty but also serve practical purposes; they can help distribute loads evenly, provide structural integrity, and even influence environmental factors like ventilation and insulation. One of the most striking examples of tessellations in architecture is the work of Antoni Gaudí. His famous Sagrada Família in Barcelona features complex tessellations that blend seamlessly into the overall Gothic-Art Nouveau design. The use of hyperboloid arches and parabolic vaults creates a sense of fluidity and continuity, mirroring the organic forms found in nature. Similarly, modern architects like Buckminster Fuller have utilized tessellations in their designs for geodesic domes, which are highly efficient structures that maximize space while minimizing materials. In contemporary architecture, tessellations continue to inspire innovative designs. The Lotus Temple in New Delhi, designed by Fariborz Sahba, is a prime example where 27 free-standing marble-clad "petals" are arranged in clusters of three to form nine sides, creating a stunning visual effect through the use of tessellations. This design not only reflects the beauty of natural forms but also enhances the spiritual and cultural significance of the temple. Moreover, advancements in technology have enabled architects to explore new dimensions of tessellations. Computational design tools allow for the creation of complex patterns that were previously impossible to achieve manually. This has led to the development of parametric architecture, where algorithms generate intricate tessellations that can be used for everything from façade design to urban planning. In conclusion, the intersection of nature and architecture through tessellations is a rich and evolving field. From ancient mosaics to modern computational designs, tessellations have provided architects with a versatile tool for creating structures that are both aesthetically captivating and functionally superior. As we continue to explore and understand the intricate patterns of nature, it is likely that we will see even more innovative applications of tessellations in architecture, further blurring the lines between the natural and built environments.