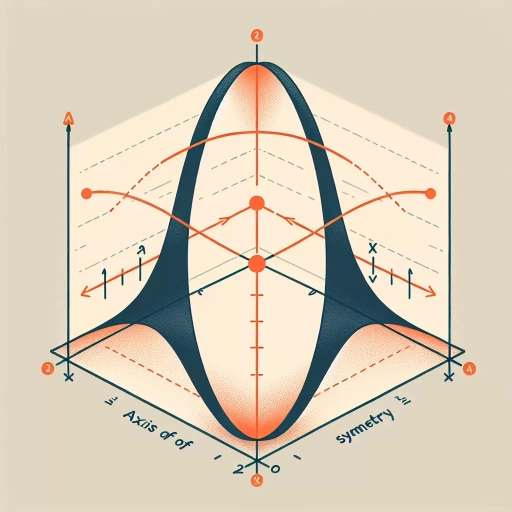
The concept of axis of symmetry is a fundamental principle in mathematics and geometry, playing a crucial role in understanding the properties and behaviors of various shapes and functions. This concept is not only essential for theoretical comprehension but also has practical applications across diverse fields such as physics, engineering, and art. In this article, we will delve into the multifaceted nature of the axis of symmetry, beginning with an in-depth exploration of **Understanding the Concept of Axis of Symmetry**. Here, we will clarify the definition and identify key characteristics that define this mathematical concept. We will then proceed to **Mathematical Representation and Calculation**, where we will discuss how to mathematically represent and calculate the axis of symmetry for different types of functions and shapes. Finally, we will examine **Applications and Importance in Various Fields**, highlighting how this concept is utilized in real-world scenarios to solve problems and create innovative solutions. By understanding these aspects, readers will gain a comprehensive insight into the significance and utility of the axis of symmetry. Let us start by grasping the foundational idea behind this concept in **Understanding the Concept of Axis of Symmetry**.

Understanding the Concept of Axis of Symmetry

Understanding the concept of axis of symmetry is a fundamental aspect of geometry and mathematics, offering insights into the structure and properties of various shapes. This concept is multifaceted, encompassing several key areas that collectively provide a comprehensive understanding. First, it is essential to grasp the definition and basic principles of axis of symmetry, which form the foundation of this concept. Here, we delve into what constitutes an axis of symmetry and how it is determined for different geometric figures. Next, we explore the various types of symmetry in geometry, including line symmetry, rotational symmetry, and reflection symmetry, each with its unique characteristics and applications. Finally, we examine real-world examples of symmetry, highlighting how this mathematical concept manifests in nature, architecture, and design. By understanding these three dimensions—definition and basic principles, types of symmetry, and real-world examples—we can appreciate the profound impact of axis of symmetry on our understanding of the world around us. Let us begin by exploring the definition and basic principles that underpin this crucial concept.

Definition and Basic Principles

The concept of axis of symmetry is rooted in the fundamental principles of geometry and algebra, providing a crucial tool for understanding and analyzing various shapes and functions. At its core, the axis of symmetry is an imaginary line that divides a figure or graph into two mirror-image halves. This definition underscores the inherent symmetry, where each point on one side of the axis corresponds to a point on the other side, equidistant from the axis. To grasp this concept fully, it is essential to delve into its basic principles. In geometry, an axis of symmetry can be found in various shapes such as lines, circles, ellipses, and polygons. For instance, a circle has an infinite number of axes of symmetry passing through its center, while an ellipse has two axes of symmetry intersecting at its center. In the case of polygons like squares and rectangles, the axes of symmetry are lines that bisect the shape into congruent parts. In algebra, particularly in the study of functions, the axis of symmetry plays a pivotal role in understanding quadratic functions. The vertex form of a quadratic function \(y = a(x - h)^2 + k\) reveals that the axis of symmetry is given by the vertical line \(x = h\). This line passes through the vertex of the parabola and divides it into two symmetric parts. For example, if we have a quadratic function \(y = x^2 - 4x + 3\), converting it to vertex form yields \(y = (x - 2)^2 - 1\), indicating that the axis of symmetry is \(x = 2\). The practical application of these principles extends beyond theoretical mathematics. In engineering and architecture, understanding axes of symmetry is crucial for designing structures that are balanced and aesthetically pleasing. For instance, many iconic buildings and monuments exhibit symmetry along one or more axes, enhancing their visual appeal and structural integrity. Moreover, in physics and chemistry, symmetry principles are fundamental in describing the behavior of particles and molecules. The concept of symmetry helps in predicting properties such as molecular structure and reactivity. For example, in crystallography, understanding the symmetry of crystal lattices is essential for determining their physical properties. In conclusion, the axis of symmetry is not just a mathematical concept but a powerful tool that permeates various fields of science and engineering. By understanding its definition and basic principles, one can appreciate the intricate balance and harmony that underlie many natural phenomena and human creations. Whether in geometry, algebra, or applied sciences, recognizing axes of symmetry enhances our ability to analyze, predict, and create symmetrical structures that are both functional and visually appealing. This foundational knowledge serves as a cornerstone for deeper explorations into more complex mathematical and scientific concepts.

Types of Symmetry in Geometry

In the realm of geometry, symmetry is a fundamental concept that underpins the beauty and order of shapes. There are several types of symmetry, each contributing to our understanding of geometric figures and their properties. **Line Symmetry**, also known as reflection symmetry, occurs when a shape can be divided into two identical halves by a line. This line is called the axis of symmetry, and it acts as a mirror line where one half of the shape reflects the other half. For example, a rectangle has two lines of symmetry: one vertical and one horizontal. **Rotational Symmetry** involves rotating a shape around a central point (the center of rotation) to produce an identical image. The number of times this can be done within a full 360-degree rotation defines the order of rotational symmetry. For instance, an equilateral triangle has rotational symmetry of order three because it looks the same after being rotated by 120 degrees. **Glide Symmetry** combines reflection and translation. Here, a shape is reflected over a line and then translated along that line to produce an identical image. This type of symmetry is less common but crucial in understanding more complex geometric patterns. **Translational Symmetry** occurs when a shape can be translated (moved) along a line to produce an identical image. This type is often seen in tessellations where shapes are repeated without overlapping. Understanding these types of symmetry is essential for grasping the concept of axis of symmetry. The axis of symmetry serves as a reference point or line around which reflections occur, making it pivotal in identifying and analyzing symmetric shapes. By recognizing these different forms of symmetry, mathematicians and geometers can classify shapes more accurately and explore their properties in depth. Moreover, symmetry plays a significant role in various fields beyond geometry, such as art, architecture, and physics. In art, symmetry can create balance and harmony; in architecture, it can enhance aesthetic appeal; and in physics, it helps describe the behavior of particles and systems. In conclusion, the various types of symmetry—line, rotational, glide, and translational—form the backbone of geometric analysis. Each type offers unique insights into how shapes are structured and how they can be transformed while maintaining their essential characteristics. By mastering these concepts, one gains a deeper appreciation for the intricate beauty and order inherent in geometric figures, ultimately enriching their understanding of the axis of symmetry and its role in geometry.

Real-World Examples of Symmetry

Symmetry, a fundamental concept in mathematics and nature, is omnipresent in various real-world examples, illustrating the axis of symmetry in diverse contexts. One of the most striking examples is found in architecture, where buildings like the Taj Mahal and the White House are designed with perfect bilateral symmetry. The central axis running through these structures divides them into two mirror-image halves, reflecting the beauty and balance that symmetry brings. In biology, the human body is another prime example; when a line is drawn down the middle of the body, it divides into two symmetrical halves, each side mirroring the other in terms of skeletal structure and organ placement. This bilateral symmetry is crucial for balance and movement. In art, symmetry is a key element in creating visually appealing compositions. For instance, Leonardo da Vinci's famous drawing "Vitruvian Man" depicts a nude figure inscribed within a circle and square, demonstrating the perfect proportions and symmetries of the human form according to Vitruvius' principles. This artwork not only showcases artistic skill but also highlights the mathematical underpinnings of symmetry. Nature itself is replete with examples of symmetry. Flowers often exhibit radial symmetry, where petals are arranged around a central axis in a repeating pattern. The intricate designs on butterfly wings and the spiral patterns on seashells also exemplify this concept. In physics, the laws governing the behavior of particles and forces are often symmetric under certain transformations, such as rotational symmetry in quantum mechanics or time-reversal symmetry in classical mechanics. In engineering, symmetry plays a critical role in design for stability and efficiency. For example, aircraft wings are designed to be symmetrical about their longitudinal axis to ensure even lift distribution during flight. Similarly, bridges like the Golden Gate Bridge in San Francisco are built with symmetrical arches to distribute weight evenly and enhance structural integrity. Even in everyday objects, symmetry can be observed. A typical bicycle wheel has rotational symmetry around its central axis; when rotated by any angle, it looks the same as it did initially. This property ensures smooth movement and balance while riding. Understanding these real-world examples helps solidify the concept of axis of symmetry by illustrating how it manifests across different domains—from art to engineering—and underscores its importance in creating balance, beauty, and functionality. By recognizing these instances of symmetry in our daily lives and natural world, we can better appreciate the mathematical principles that govern them and apply these insights to various fields of study and practical applications.

Mathematical Representation and Calculation

Mathematical representation and calculation are fundamental pillars in understanding and analyzing various mathematical concepts. These tools enable us to express complex ideas in a clear and concise manner, facilitating deeper insights and precise solutions. In this article, we will delve into three key aspects that underscore the importance of mathematical representation and calculation: Equations and Formulas for Axis of Symmetry, Graphical Analysis and Visualization, and Step-by-Step Calculation Examples. Firstly, understanding the equations and formulas for the axis of symmetry is crucial for identifying and analyzing symmetric properties in functions. This concept is pivotal in algebra and geometry, allowing us to determine the line about which a graph is symmetric. Secondly, graphical analysis and visualization provide a visual framework for interpreting data and functions, making abstract concepts more tangible and easier to comprehend. Lastly, step-by-step calculation examples serve as practical guides, illustrating how to apply mathematical principles to solve problems systematically. By exploring these three areas, we can gain a comprehensive understanding of how mathematical representation and calculation interplay to enhance our analytical skills. Let us begin by examining the essential equations and formulas for determining the axis of symmetry, a foundational concept that sets the stage for more advanced mathematical explorations.

Equations and Formulas for Axis of Symmetry

The axis of symmetry is a fundamental concept in mathematics, particularly in geometry and algebra, which helps in understanding the symmetry properties of various shapes and functions. Mathematically, the axis of symmetry can be represented and calculated using specific equations and formulas that depend on the type of object or function being analyzed. For a parabola given by the quadratic equation \(y = ax^2 + bx + c\), the axis of symmetry is a vertical line that divides the parabola into two equal halves. The equation for the axis of symmetry of a parabola is \(x = -\frac{b}{2a}\). This formula is derived from the vertex form of a parabola, where the vertex \((h, k)\) lies on the axis of symmetry, and \(h = -\frac{b}{2a}\). Understanding this equation allows for precise identification and calculation of the axis of symmetry, which is crucial in graphing parabolas accurately. In the context of functions, particularly even functions like \(f(x) = f(-x)\), the axis of symmetry is often the y-axis. For example, the function \(f(x) = x^2\) has an axis of symmetry at \(x = 0\), because \(f(x) = f(-x)\) holds true for all \(x\). This property can be generalized to other even functions, where the axis of symmetry is always the y-axis. For more complex shapes like ellipses and hyperbolas, which are represented by conic sections, the axes of symmetry are determined by their respective equations. For an ellipse given by \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\), the axes of symmetry are the major and minor axes, which are the lines \(x = 0\) and \(y = 0\). Similarly, for a hyperbola given by \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), the axes of symmetry are also the x-axis and y-axis. In three-dimensional geometry, the concept extends to planes of symmetry for objects like cones and pyramids. For instance, a right circular cone has a plane of symmetry that passes through its apex and is perpendicular to its base. The mathematical representation and calculation of these axes or planes of symmetry are essential tools in various fields such as physics, engineering, and architecture. They help in understanding and predicting the behavior of physical systems, designing symmetric structures, and analyzing data sets that exhibit symmetry. In summary, the equations and formulas for determining the axis of symmetry provide a robust framework for analyzing and understanding symmetric properties across different mathematical objects. Whether it's a simple quadratic equation or a complex conic section, these mathematical tools enable precise calculations and visualizations that are fundamental to many scientific and practical applications.

Graphical Analysis and Visualization

Graphical analysis and visualization are indispensable tools in understanding and interpreting mathematical concepts, particularly when exploring the axis of symmetry. These techniques enable us to transform abstract mathematical representations into tangible, visual forms that facilitate deeper comprehension and insight. By plotting functions on a coordinate plane, we can visually identify key features such as maxima, minima, and points of inflection, which are crucial for determining the axis of symmetry. For instance, in the context of quadratic functions, graphical analysis allows us to see the parabolic shape of the graph and identify its vertex. The axis of symmetry for a quadratic function is a vertical line that passes through the vertex, dividing the parabola into two symmetric halves. This visual representation makes it clear that any point on one side of the axis has a corresponding point on the other side, equidistant from the axis. This symmetry is not just aesthetically pleasing but also mathematically significant, as it helps in solving equations and understanding the behavior of the function. Moreover, graphical visualization extends beyond simple functions to more complex mathematical structures such as polynomial functions, trigonometric functions, and even three-dimensional surfaces. For example, in three-dimensional space, visualizing surfaces like paraboloids or ellipsoids helps in identifying their axes of symmetry, which are essential for understanding their geometric properties and applications in fields like physics and engineering. The use of technology, such as graphing calculators and computer software, has further enhanced our ability to perform graphical analysis. These tools allow for rapid plotting of functions and enable interactive exploration of graphs, making it easier to experiment with different parameters and observe how they affect the axis of symmetry. This interactivity fosters a more intuitive understanding of mathematical concepts by allowing users to see how changes in the function's parameters impact its graphical representation. In addition to enhancing understanding, graphical analysis also aids in problem-solving. By visualizing data or functions, one can often identify patterns or anomalies that might be difficult to discern from raw numerical data or algebraic expressions alone. For instance, in statistical analysis, visualizing data distributions can reveal skewness or outliers that could significantly impact calculations involving symmetry. In conclusion, graphical analysis and visualization are powerful complements to mathematical representation and calculation when studying the axis of symmetry. They provide a clear and intuitive way to understand complex mathematical concepts by transforming them into visual representations that highlight key features and relationships. This synergy between visual and algebraic methods ensures a more comprehensive and engaging learning experience, making it easier to grasp and apply mathematical principles effectively.

Step-by-Step Calculation Examples

When delving into the concept of the axis of symmetry, particularly in the context of mathematical representation and calculation, it is crucial to understand how step-by-step calculations can elucidate this fundamental idea. The axis of symmetry is a line that divides a shape or graph into two mirror-image halves. Here, we will explore step-by-step calculation examples to illustrate this concept clearly. ### Step-by-Step Calculation Examples #### Example 1: Finding the Axis of Symmetry for a Quadratic Function Consider the quadratic function \( f(x) = ax^2 + bx + c \). The axis of symmetry for this function can be found using the formula \( x = -\frac{b}{2a} \). Let's take the function \( f(x) = 2x^2 + 4x + 3 \). 1. **Identify Coefficients**: Here, \( a = 2 \) and \( b = 4 \). 2. **Apply the Formula**: Substitute these values into the formula for the axis of symmetry. \[ x = -\frac{4}{2 \times 2} = -\frac{4}{4} = -1 \] 3. **Interpretation**: The axis of symmetry for the function \( f(x) = 2x^2 + 4x + 3 \) is the vertical line \( x = -1 \). #### Example 2: Determining the Axis of Symmetry for a Parabola For a parabola given in vertex form \( f(x) = a(x - h)^2 + k \), the axis of symmetry is simply \( x = h \), where \( (h, k) \) is the vertex of the parabola. 1. **Given Parabola**: Consider \( f(x) = 3(x - 2)^2 + 5 \). 2. **Identify Vertex**: Here, \( h = 2 \) and \( k = 5 \). 3. **Axis of Symmetry**: The axis of symmetry is \( x = 2 \). #### Example 3: Finding the Axis of Symmetry for an Ellipse For an ellipse centered at \( (h, k) \) with major axis parallel to the x-axis, the equation is of the form \( \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 \). The axis of symmetry in this case is the vertical line through the center, given by \( x = h \). 1. **Given Ellipse**: Consider \( \frac{(x - 3)^2}{4} + \frac{(y - 1)^2}{9} = 1 \). 2. **Identify Center**: Here, \( h = 3 \) and \( k = 1 \). 3. **Axis of Symmetry**: The axis of symmetry is \( x = 3 \). ### Conclusion These step-by-step examples illustrate how different mathematical representations—quadratic functions, parabolas in vertex form, and ellipses—can be used to calculate their respective axes of symmetry. By applying specific formulas and identifying key parameters such as coefficients or vertices, one can accurately determine these lines that reflect the symmetry inherent in these geometric shapes. This methodical approach not only enhances understanding but also provides a practical toolkit for solving problems involving symmetry in various mathematical contexts.

Applications and Importance in Various Fields

The applications and importance of various fields are multifaceted and far-reaching, influencing a wide array of disciplines. This article delves into the significant roles these fields play in geometry and algebra, their critical applications in physics and engineering, and their profound impact on art and design. In geometry and algebra, these fields provide the foundational tools for understanding spatial relationships and solving complex equations, which are essential for advancements in mathematics. In physics and engineering, they enable the development of theories and models that govern our understanding of the universe and the creation of innovative technologies. Additionally, in art and design, these fields inspire creativity and precision, allowing artists to create visually stunning and mathematically accurate works. By exploring these diverse applications, we can appreciate the interconnectedness and importance of these fields in shaping our world. Let us begin by examining the role of these fields in geometry and algebra, where the very fabric of mathematical reasoning is woven.

Role in Geometry and Algebra

The axis of symmetry plays a pivotal role in both geometry and algebra, serving as a fundamental concept that bridges these two disciplines. In geometry, the axis of symmetry is a line that divides a shape into two mirror-image halves. For example, in the case of a parabola, the axis of symmetry is a vertical line that passes through the vertex and is equidistant from corresponding points on either side of the parabola. This concept is crucial for understanding and analyzing symmetric shapes such as circles, ellipses, and polygons. It helps in identifying properties like reflection and rotational symmetry, which are essential in various geometric transformations and constructions. In algebra, particularly in the study of quadratic equations and functions, the axis of symmetry is instrumental. For a quadratic function \(f(x) = ax^2 + bx + c\), the axis of symmetry can be found using the formula \(x = -\frac{b}{2a}\). This line represents the vertical axis around which the parabola opens or closes, providing valuable insights into the function's behavior and key features such as its vertex and turning points. Understanding this concept allows algebraists to graph quadratic functions accurately and analyze their properties, which is vital for solving problems in physics, engineering, economics, and other fields where quadratic models are used to describe real-world phenomena. The interplay between geometry and algebra through the axis of symmetry also extends to more advanced mathematical concepts. For instance, in coordinate geometry, identifying the axis of symmetry helps in determining the equations of curves and surfaces. In calculus, it aids in finding maxima and minima of functions by identifying critical points along the axis of symmetry. This dual role underscores the importance of the axis of symmetry as a unifying thread that ties together various mathematical disciplines. Moreover, the applications of the axis of symmetry are not limited to pure mathematics; they permeate various fields such as architecture, design, physics, and engineering. Architects use symmetry to create aesthetically pleasing and balanced structures. In physics, the concept of symmetry is central to understanding laws of motion and conservation principles. Engineers rely on symmetric designs for stability and efficiency in structures like bridges and buildings. The axis of symmetry thus becomes a critical tool for problem-solving across diverse domains, highlighting its significance beyond mere theoretical mathematics. In conclusion, the axis of symmetry is a cornerstone concept that integrates geometric and algebraic principles, facilitating deeper understanding and practical applications across multiple fields. Its importance lies not only in its theoretical significance but also in its widespread applicability, making it an indispensable tool for anyone working within or intersecting with mathematical disciplines.

Applications in Physics and Engineering

The axis of symmetry, a fundamental concept in geometry and algebra, finds extensive applications in both physics and engineering, underscoring its importance across various fields. In physics, the axis of symmetry plays a crucial role in understanding the behavior of physical systems. For instance, in rotational mechanics, the axis of symmetry is essential for determining the moment of inertia of an object. This concept is vital for calculating rotational kinetic energy and torque, which are fundamental in the study of rotating systems such as wheels, gears, and turbines. Additionally, in quantum mechanics, symmetry principles are used to predict the properties of particles and systems, helping physicists understand phenomena like particle decay and nuclear reactions. In engineering, the axis of symmetry is a cornerstone for designing and analyzing structures. Structural engineers rely on symmetry to simplify calculations and ensure that buildings and bridges can withstand various loads without collapsing. For example, symmetrical structures distribute stress more evenly, enhancing stability and reducing the risk of failure. In mechanical engineering, the axis of symmetry is critical for the design of engines, pumps, and other machinery where rotational balance is essential for efficient operation and longevity. Aerospace engineers also utilize symmetry principles to optimize the aerodynamic performance of aircraft and spacecraft, ensuring stable flight and minimizing drag. Moreover, in materials science and nanotechnology, understanding the symmetry of crystal structures is pivotal for predicting material properties such as strength, conductivity, and optical behavior. This knowledge is crucial for developing new materials with specific characteristics tailored for various applications. In biomedical engineering, symmetry principles are applied in the design of prosthetics and implants to ensure proper fit and function within the human body. The importance of the axis of symmetry extends to computational methods as well. In computational fluid dynamics (CFD) and finite element analysis (FEA), symmetry is exploited to reduce computational complexity by simplifying models and boundary conditions. This not only speeds up simulations but also enhances accuracy by focusing on critical regions of interest. In conclusion, the axis of symmetry is not merely a theoretical concept; it has profound practical implications across physics and engineering. Its applications span from fundamental research in quantum mechanics to practical design in structural and mechanical engineering. By leveraging symmetry principles, scientists and engineers can develop more efficient, stable, and innovative solutions that underpin modern technology and infrastructure. This underscores the significance of understanding and applying the axis of symmetry in various fields, highlighting its role as a foundational element in scientific and engineering endeavors.

Impact on Art and Design

The concept of axis of symmetry has profound implications for art and design, influencing various aspects of creative expression and visual composition. In art, symmetry is often used to create a sense of balance, harmony, and order. Artists leverage the axis of symmetry to divide their work into mirror-image halves, enhancing the aesthetic appeal and structural integrity of the piece. For instance, in architecture, symmetrical designs are prevalent in historical buildings and monuments, such as the Taj Mahal or the White House, where the central axis of symmetry contributes to their grandeur and symmetry. This principle is also crucial in graphic design, where it helps in creating logos, icons, and other visual elements that are visually appealing and memorable. The use of symmetry in art can evoke emotions and convey meaning; for example, bilateral symmetry can suggest stability and perfection, while asymmetry can introduce dynamism and creativity. In design fields like interior design and product design, understanding the axis of symmetry is essential for creating balanced and functional spaces or products. Interior designers use symmetry to arrange furniture and decor in a way that feels cohesive and inviting. Similarly, product designers apply symmetry to ensure that their creations are both aesthetically pleasing and functional. For instance, the design of a chair or a table often relies on symmetry to achieve stability and visual appeal. Moreover, the concept extends into digital art and animation. In computer-aided design (CAD) software, understanding axes of symmetry allows designers to create complex models efficiently by mirroring elements across these axes. This technique is particularly useful in fields like engineering and automotive design where precision is paramount. The impact of axis of symmetry on art and design also intersects with psychological and cultural aspects. Symmetrical compositions can evoke feelings of calmness and trustworthiness, which is why they are often used in branding and advertising. Additionally, cultural symbols and motifs frequently incorporate symmetrical patterns to convey unity and balance. In conclusion, the axis of symmetry plays a pivotal role in shaping artistic and design principles across various disciplines. By leveraging this concept, artists and designers can create works that are not only visually striking but also emotionally resonant and functionally sound. Whether it's in architecture, graphic design, or product design, understanding the axis of symmetry is crucial for achieving balance, harmony, and aesthetic excellence. This fundamental principle underscores the importance of symmetry in enhancing both the beauty and functionality of creative works.