In the vast and intricate world of physics and mathematics, the concept of a ray plays a pivotal role in understanding various phenomena and applications. A ray, fundamentally, is a line that extends infinitely in one direction from a single point, known as the endpoint. This simple yet powerful concept has far-reaching implications across multiple fields, from optics and geometry to engineering and computer graphics. In this article, we will delve into the definition and basic concepts of a ray, exploring its foundational principles and how it is defined within different contexts. We will also examine the diverse applications of rays in various fields, highlighting their significance in real-world scenarios. Finally, we will provide real-world examples and practical uses of rays, illustrating how this abstract concept translates into tangible benefits. By understanding what a ray is and its multifaceted applications, we can appreciate the profound impact it has on our daily lives and technological advancements. Let us begin by defining and exploring the basic concepts of a ray.

Definition and Basic Concepts of a Ray

In the realm of geometry, understanding the fundamental concepts is crucial for grasping more complex theories and applications. One such foundational element is the ray, a concept that, while simple, forms the backbone of various geometric principles. This article delves into the definition and basic concepts of a ray, providing a comprehensive overview that is both informative and engaging. We will explore the mathematical definition of a ray, which lays out the precise criteria for what constitutes a ray in geometric terms. Additionally, we will examine the geometric representation of rays, highlighting how they are visualized and utilized in spatial contexts. Finally, we will clarify the often-confused distinction between rays and lines, ensuring a clear understanding of these related yet distinct geometric entities. By the end of this article, readers will have a solid grasp of the definition and basic concepts of a ray, equipping them with a robust foundation in geometric principles.

Mathematical Definition of a Ray

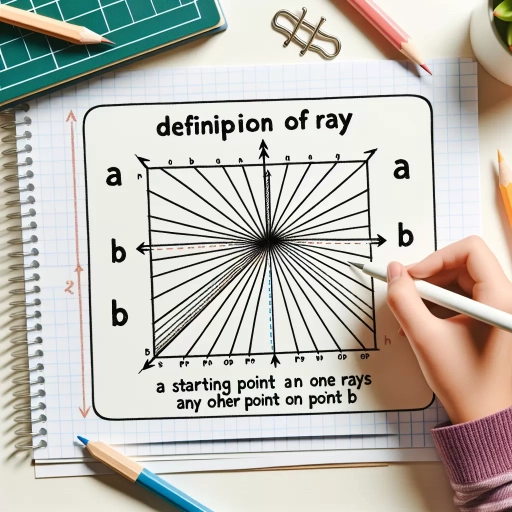
In the realm of geometry, a ray is a fundamental concept that extends our understanding of lines and points. Mathematically, a ray is defined as a line segment that extends infinitely in one direction from a single point, known as the endpoint or origin. This definition distinguishes a ray from a line, which extends infinitely in both directions, and from a line segment, which has two endpoints and a finite length. To be precise, consider a point \(A\) in a geometric space. A ray originating from \(A\) can be thought of as starting at \(A\) and extending outward indefinitely in one specific direction. This direction is often specified by another point \(B\), which lies on the ray. The notation for this ray is typically denoted as \(\overrightarrow{AB}\) or simply \(AB\), indicating that it starts at \(A\) and extends towards \(B\) without bound. The key characteristics of a ray include its endpoint (the starting point) and its direction. Two rays are considered equal if they share the same endpoint and direction, regardless of how far they extend. This concept is crucial in various geometric constructions and proofs, where the direction and starting point of a ray can significantly impact the outcome. Rays are also integral in defining angles and measuring their sizes. For instance, two rays originating from the same point form an angle, with the vertex being the common endpoint. The measure of this angle depends on the direction of these rays relative to each other. In practical applications, rays are used extensively in fields such as optics, where light travels in straight lines (rays) until it encounters an obstacle or medium change. Similarly, in computer graphics, rays are used to simulate lighting effects by tracing paths of light from an object to the observer's eye. Understanding rays is essential for advanced geometric concepts like half-planes and convex sets. For example, a half-plane can be defined by a line and one of its associated rays, indicating which side of the line belongs to the half-plane. In summary, the mathematical definition of a ray provides a robust framework for understanding geometric relationships and directions within space. Its precise definition as an infinitely extending line segment from a single point underpins many theoretical and practical applications across various disciplines. By grasping this fundamental concept, one can better navigate more complex geometric theories and real-world problems involving spatial relationships and directions.

Geometric Representation

Geometric representation is a fundamental aspect of understanding and visualizing mathematical concepts, particularly when defining and exploring the basic concepts of a ray. In geometry, a ray is often depicted as an arrow extending infinitely in one direction from a single point, known as the endpoint or origin. This visual representation helps in grasping the abstract nature of a ray, which is essentially a line segment that has no end but has a definite starting point. To create an engaging and informative paragraph about geometric representation in the context of defining a ray, one must delve into how these visual tools enhance comprehension. For instance, when students first encounter the concept of a ray, they might find it challenging to conceptualize something that extends infinitely. However, through geometric representation—using diagrams and illustrations—a ray becomes tangible. The arrowhead symbolizes the direction in which the ray extends, while the endpoint clearly marks where it begins. This visual aid not only clarifies the definition but also facilitates understanding of related concepts such as angles, intersections, and parallel lines. Moreover, geometric representation allows for the exploration of various properties and relationships involving rays. For example, when two rays intersect at their endpoints, they form an angle. Visualizing this intersection point helps in understanding how angles are measured and classified. Additionally, geometric representations can illustrate how multiple rays can emanate from a single point, forming different angles and spatial relationships. These visualizations are crucial for advanced geometric concepts such as trigonometry and spatial geometry. In educational settings, geometric representations of rays are often used in conjunction with other visual tools like coordinate planes and graphs. These tools collectively provide a comprehensive framework for understanding geometric principles. By combining theoretical definitions with practical visualizations, learners can transition smoothly from abstract concepts to practical applications. For instance, in engineering and architecture, precise geometric representations are essential for designing structures where accurate measurements and spatial relationships are critical. In summary, geometric representation plays a pivotal role in defining and understanding the basic concepts of a ray. Through clear and engaging visualizations, learners can grasp complex abstract ideas more effectively. This approach not only enhances comprehension but also fosters deeper insights into related geometric principles, making it an indispensable tool in both educational and professional contexts. By leveraging these visual aids, individuals can build a robust foundation in geometry that supports further exploration and application of mathematical concepts.

Difference Between Rays and Lines

In the realm of geometry, understanding the distinction between rays and lines is fundamental, as these concepts form the building blocks of more complex geometric structures. A **line** is a set of points that extend infinitely in two directions. It has no beginning or end and can be thought of as a straight path that continues forever. Lines are often represented by two points on the line, denoted as \( \overline{AB} \), where A and B are any two points on the line. This representation emphasizes that a line is a continuous, unbounded entity. On the other hand, a **ray** is a part of a line that extends infinitely in one direction from a single point, known as the endpoint or initial point. Unlike lines, rays have a definite starting point but no ending point; they stretch out indefinitely in one direction. For example, if we consider a ray starting from point A and extending through point B, it would be denoted as \( \overrightarrow{AB} \). Here, A is the endpoint (or initial point), and the ray extends infinitely beyond B. The key differences between rays and lines lie in their extent and direction. While a line extends infinitely in both directions without any endpoint, a ray extends infinitely in only one direction from its initial point. This distinction is crucial for various geometric applications, such as defining angles and determining spatial relationships between objects. To illustrate further, consider an analogy: imagine a line as an endless highway that you can travel on in either direction without ever reaching an end. In contrast, a ray is like a one-way street that starts at a specific point (the endpoint) and continues indefinitely in one direction but does not allow travel in the opposite direction. Understanding these differences is essential for advanced geometric concepts and real-world applications. For instance, in physics and engineering, rays are used to model light paths or trajectories of objects moving in a straight line from a fixed starting point. In contrast, lines are often used to represent boundaries or paths that can be traversed in either direction. In summary, while both lines and rays are fundamental geometric entities representing straight paths, they differ significantly in terms of their extent and direction. Lines are infinite in both directions with no endpoints, whereas rays are infinite in one direction with a single endpoint. This clear distinction is vital for precise communication and problem-solving across various fields that rely on geometric principles.

Applications of Rays in Various Fields

Rays, fundamental concepts in various scientific and technological fields, play a crucial role in understanding and applying principles across diverse disciplines. From the intricate world of physics and optics, where rays help explain the behavior of light and its interactions with matter, to the precise realm of geometry and mathematics, where rays are essential in defining lines and planes, their significance is undeniable. Additionally, in the dynamic field of computer graphics and engineering, rays are pivotal in rendering realistic images and simulating real-world environments. This article delves into these applications, exploring how rays are utilized in physics and optics to study light propagation, in geometry and mathematics to establish foundational concepts, and in computer graphics and engineering to create immersive visual experiences. By examining these diverse applications, we will transition seamlessly into a deeper exploration of the definition and basic concepts of a ray, providing a comprehensive understanding of this versatile and essential concept.

Rays in Physics and Optics

In the realm of physics and optics, rays are fundamental concepts that underpin our understanding of light and its behavior. A ray is essentially a line that represents the path along which light travels, simplifying the complex nature of light into a more manageable and visualizable form. This abstraction is crucial for analyzing and predicting the behavior of light in various optical systems. In physics, rays are used to describe the propagation of light through different media, such as air, water, or glass, allowing us to study phenomena like refraction, reflection, and diffraction. For instance, Snell's Law, which governs refraction, relies on the concept of rays to explain how light bends as it passes from one medium to another. In optics, the study of rays is indispensable for designing and optimizing optical instruments like lenses, mirrors, and telescopes. By tracing the paths of light rays through these systems, scientists can determine focal lengths, image formation, and aberrations. This knowledge is pivotal in creating high-quality optical devices that are essential in fields such as astronomy, where precise imaging is critical for observing distant celestial objects. Additionally, ray tracing techniques are employed in ophthalmology to understand vision defects and design corrective lenses that can restore clear vision. Beyond these traditional applications, the concept of rays extends into modern technologies. In computer graphics, ray tracing algorithms simulate the way light interacts with virtual objects to produce realistic images and scenes. This technique is used extensively in film production, video games, and architectural visualization to create lifelike environments. Furthermore, in medical imaging techniques like optical coherence tomography (OCT), rays of light are used to generate detailed cross-sectional images of tissues, aiding in diagnostics and treatment planning. The versatility of rays also makes them a cornerstone in solar energy applications. Solar concentrators and photovoltaic systems rely on the precise alignment and focusing of sunlight rays to maximize energy conversion efficiency. Understanding how rays interact with different materials and surfaces is essential for optimizing these systems and enhancing their performance. In summary, the concept of rays in physics and optics is a powerful tool that enables us to understand, predict, and manipulate the behavior of light across various fields. From the design of optical instruments to the simulation of light in computer graphics and the optimization of solar energy systems, the study of rays continues to drive innovation and advancement in multiple disciplines.

Rays in Geometry and Mathematics

In geometry and mathematics, a ray is a fundamental concept that extends infinitely in one direction from a single point, known as the endpoint or origin. Unlike line segments, which have two endpoints, rays have only one endpoint and continue indefinitely in the other direction. This unique property makes rays essential in various mathematical and real-world applications. In geometry, rays are used to define angles and to study the properties of shapes. For instance, when two rays share the same endpoint, they form an angle, which is a crucial element in trigonometry and spatial reasoning. Rays also play a significant role in the study of lines and planes, helping to establish relationships between different geometric figures. In coordinate geometry, rays can be represented using vector equations, allowing for precise calculations and visualizations. Beyond geometry, rays find extensive use in physics and engineering. In optics, light rays are used to describe the path of light as it travels through different media. This concept is pivotal in understanding phenomena such as reflection, refraction, and diffraction. In computer graphics, rays are employed in ray tracing algorithms to simulate realistic lighting effects by tracing the path of light as it interacts with objects in a scene. In navigation and surveying, rays are utilized to determine distances and directions. For example, in triangulation methods, rays from known points are used to calculate the position of unknown points. This technique is crucial for mapping terrains and establishing precise coordinates. Furthermore, rays have practical applications in fields like architecture and design. Architects use rays to analyze sunlight patterns and shadow effects on buildings, ensuring optimal natural lighting and aesthetic appeal. In urban planning, rays help in designing traffic flow patterns and pedestrian paths to enhance safety and efficiency. The versatility of rays extends into computational mathematics as well. In algorithms for solving problems involving visibility and shadowing, rays are used to determine which parts of a scene are visible from a given viewpoint. This is particularly important in video games and virtual reality applications where realistic environments need to be rendered quickly. In summary, rays are not just abstract mathematical constructs but powerful tools with diverse applications across various fields. Their ability to extend infinitely in one direction makes them indispensable for describing angles, paths of light, navigation routes, and more. Whether in theoretical geometry or practical engineering, the concept of a ray provides a robust framework for solving complex problems and understanding the world around us.

Rays in Computer Graphics and Engineering

In the realm of computer graphics and engineering, rays play a pivotal role in simulating and rendering realistic environments. The concept of rays is fundamental to various techniques such as ray tracing, which involves tracing the path of light as it bounces off different objects in a scene. This method allows for the creation of highly detailed and accurate images by accounting for reflections, refractions, and shadows. In computer graphics, rays are used to determine how light interacts with 3D models, enabling the generation of photorealistic images and animations. For instance, in film and video game production, ray tracing is employed to create lifelike scenes with accurate lighting effects, enhancing the overall visual experience. Beyond visual rendering, rays are also crucial in engineering fields like computer-aided design (CAD) and computational geometry. Here, rays are used to perform geometric queries such as collision detection and visibility testing. In CAD software, rays help designers understand how different components interact spatially, facilitating the design of complex systems like mechanical assemblies or architectural structures. Additionally, in robotics and autonomous vehicles, ray-based algorithms are utilized for obstacle detection and path planning. These algorithms simulate the environment by casting virtual rays to predict potential collisions and navigate safely. The application of rays extends further into fields like medical imaging and scientific visualization. In medical imaging techniques such as CT scans or MRI, rays are used to reconstruct detailed images of internal body structures. By tracing the path of X-rays or magnetic fields through the body, these technologies provide critical diagnostic information. Similarly, in scientific visualization, rays help researchers visualize complex data sets by projecting them onto 2D or 3D spaces, allowing for better understanding and analysis of phenomena such as fluid dynamics or molecular interactions. Moreover, the efficiency of ray-based algorithms has been significantly improved with advancements in hardware and software technologies. Modern graphics processing units (GPUs) are optimized for parallel processing, making them ideal for handling the massive computational demands of ray tracing. This has led to real-time ray tracing capabilities in various applications, from gaming to architectural walkthroughs. The integration of artificial intelligence (AI) also enhances ray-based techniques by optimizing rendering times and improving accuracy through machine learning algorithms. In summary, rays are a versatile tool in computer graphics and engineering, enabling the creation of realistic visualizations, facilitating geometric computations, and supporting critical applications across diverse fields. Their role continues to evolve with technological advancements, making them an indispensable component in modern computational methodologies.

Real-World Examples and Practical Uses of Rays

In the realm of physics and everyday life, rays play a pivotal role in various technological and practical applications. From the precision of laser technology to the intricacies of human vision and perception, and even in the meticulous field of navigation and surveying, rays are fundamental components that drive innovation and accuracy. This article delves into real-world examples and practical uses of rays, highlighting their significance across different domains. We will explore how laser technology leverages rays to achieve high-precision applications, examine the crucial role light rays play in vision and perception, and discuss how rays are utilized in navigation and surveying to ensure accurate measurements. By understanding these practical applications, we can appreciate the broader importance of rays in our daily lives. This journey into the practical uses of rays will ultimately lead us to a deeper understanding of their definition and basic concepts, providing a comprehensive overview of this essential physical phenomenon.

Laser Technology and Its Applications

Laser technology has revolutionized numerous fields with its precision, power, and versatility. At its core, a laser (Light Amplification by Stimulated Emission of Radiation) generates a concentrated beam of light through stimulated emission, offering unparalleled coherence and intensity. This technology has found widespread applications across various sectors. In **medicine**, lasers are used for both diagnostic and therapeutic purposes. For instance, laser surgery allows for precise incisions with minimal tissue damage, reducing recovery time and scarring. Laser treatments are also effective in ophthalmology for correcting vision problems such as myopia, hyperopia, and astigmatism through procedures like LASIK. Additionally, lasers are employed in dermatology to treat skin conditions like acne, scars, and pigmentation disorders. **Industrial manufacturing** heavily relies on laser technology for cutting, welding, and surface treatment. High-precision laser cutting machines can accurately cut through metals, plastics, and other materials with minimal waste and high speed. Laser welding is used in automotive and aerospace industries for joining materials without causing significant thermal distortion. Surface treatment with lasers enhances material properties such as hardness and corrosion resistance. In **telecommunications**, lasers play a crucial role in fiber optic communication systems. They convert electrical signals into light pulses that travel through fiber optic cables at incredibly high speeds, enabling fast and reliable data transmission over long distances. This technology underpins modern internet infrastructure, facilitating global connectivity. **Scientific research** also benefits from laser technology. Lasers are used in spectroscopy to analyze the composition of materials by measuring how they interact with light. In particle physics, high-energy lasers are employed to accelerate particles to near-light speeds for collision experiments. Furthermore, lasers are integral in the development of quantum computing and quantum cryptography due to their ability to manipulate photons precisely. **Consumer electronics** incorporate lasers in various products. For example, CD and DVD players use lasers to read data stored on discs. Laser printers produce high-quality text and images by precisely depositing toner onto paper. Even some gaming systems utilize laser technology for motion sensing and tracking. **Military and defense** applications include laser-guided missiles and precision targeting systems. These systems use lasers to illuminate targets, allowing missiles to home in accurately. Non-lethal laser weapons are also being developed for crowd control and other tactical uses. In **environmental monitoring**, lasers are used in LIDAR (Light Detection and Ranging) technology to create detailed topographic maps and monitor atmospheric conditions such as pollution levels and weather patterns. These diverse applications highlight the transformative impact of laser technology across multiple disciplines, demonstrating its potential to drive innovation and solve complex problems in real-world scenarios. Whether it's enhancing medical treatments, optimizing industrial processes, or advancing scientific research, lasers continue to play a pivotal role in shaping our technological landscape.

Light Rays in Vision and Perception

In the realm of vision and perception, light rays play a crucial role in how we interpret and understand our surroundings. When light from an object travels through space, it forms a collection of rays that can intersect with our eyes, allowing us to perceive the world around us. This process begins with the reflection of light off surfaces; each point on an object reflects light in various directions, creating a multitude of light rays. These rays then travel through the air until they reach our eyes, where they are focused by the lens onto the retina. Here, photoreceptor cells convert the light into electrical signals that are transmitted to the brain, which interprets these signals as visual information. The path of light rays is fundamental to understanding optical phenomena such as reflection, refraction, and diffraction. For instance, when light rays hit a mirror, they reflect back at the same angle they hit the surface, allowing us to see our reflections. In contrast, when light passes from one medium to another (like from air into water), it bends due to refraction, which is why objects appear distorted when submerged. These principles are not just theoretical; they have practical applications in everyday life. For example, corrective lenses like glasses and contact lenses work by refracting light rays to correct vision impairments such as myopia or hyperopia. Moreover, the study of light rays has led to significant advancements in technology. In photography, understanding how light rays interact with lenses and sensors is essential for capturing high-quality images. The design of camera lenses involves careful consideration of how to focus and manipulate light rays to achieve desired effects such as depth of field or bokeh. Similarly, in medical imaging techniques like optical coherence tomography (OCT), precise control over light rays allows for detailed imaging of internal structures without invasive procedures. In addition to these technological applications, the behavior of light rays also influences architectural design. Architects often use principles of optics to create visually appealing and functional spaces. For instance, the placement of windows and mirrors can be optimized to maximize natural light and create illusions of larger spaces by strategically reflecting light rays. In conclusion, the study of light rays in vision and perception is not only fascinating but also highly practical. It underpins many real-world applications from corrective vision to advanced imaging technologies and even architectural design. Understanding how light interacts with our environment enables us to harness its power more effectively, enhancing both our daily experiences and the tools we use to navigate the world around us.

Rays in Navigation and Surveying

In the realms of navigation and surveying, rays play a crucial role in determining precise locations, orientations, and distances. A ray, defined as a line extending infinitely in one direction from a single point, is instrumental in various real-world applications. For instance, in navigation systems such as GPS (Global Positioning System), rays are used to calculate the user's position. Here, multiple satellites emit signals that form rays which intersect at the receiver's location, allowing for triangulation and accurate positioning. This principle is also applied in geodetic surveying where rays from known reference points help in establishing the coordinates of new points on the Earth's surface. In maritime navigation, rays are essential for determining bearings and distances to landmarks or other vessels. Lighthouses emit light rays that serve as visual aids for sailors to navigate through treacherous waters. Similarly, radar systems use electromagnetic rays to detect and locate objects, providing critical information for safe navigation. In land surveying, rays are used in techniques like triangulation and trilateration. By measuring the angles formed by rays connecting known points (triangulation) or the lengths of rays between points (trilateration), surveyors can accurately map out large areas with high precision. This is particularly important for urban planning, boundary disputes, and infrastructure projects where precise measurements are paramount. Furthermore, in photogrammetry—a discipline that involves extracting information from photographs—rays are used to reconstruct three-dimensional models from overlapping images. By tracing the rays that connect corresponding points on different photographs back to their intersection points in space, photogrammetrists can create detailed topographic maps and 3D models of terrain. The practical uses of rays extend into engineering as well. In construction projects, laser leveling tools emit rays to ensure that surfaces are perfectly level or aligned according to design specifications. These tools rely on the principle that a ray maintains its direction indefinitely unless interrupted by an obstacle or reflected off a surface. In summary, rays are fundamental components in various navigation and surveying techniques due to their ability to define precise directions and distances. From GPS technology to maritime navigation, land surveying, photogrammetry, and construction engineering, the application of rays ensures accuracy and reliability in a wide range of critical tasks. Their versatility underscores their importance as a foundational concept in these fields.