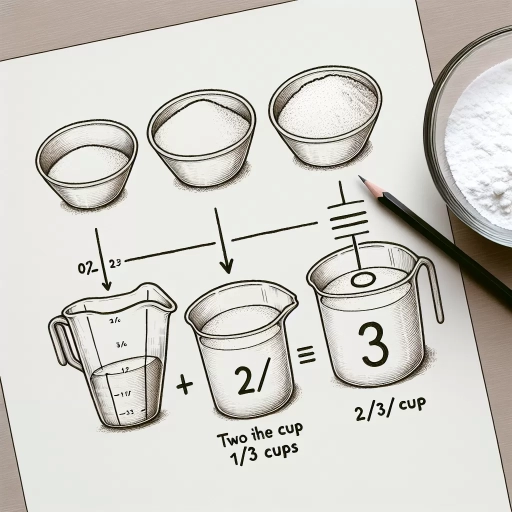
When working with recipes or measuring ingredients, understanding how to double measurements is a crucial skill. One common query that arises is what happens when you double a fraction of a cup, specifically 1/3 cup. This article delves into the concept of doubling measurements, providing a comprehensive guide on how to calculate and apply this knowledge in practical scenarios. We will begin by **Understanding the Concept of Doubling a Measurement**, which lays the foundation for accurately scaling up ingredients. Next, we will dive into **Calculating 1/3 Cup Doubled**, where we will break down the steps to arrive at the correct measurement. Finally, we will explore **Practical Applications and Examples**, highlighting how this skill can be applied in everyday cooking and baking. By the end of this article, you will be well-equipped to handle any measurement doubling task with confidence. Let's start by grasping the fundamental concept of doubling measurements.

Understanding the Concept of Doubling a Measurement

Understanding the concept of doubling a measurement is a fundamental skill that underpins various aspects of everyday life, from cooking and construction to science and engineering. This article delves into the intricacies of doubling measurements, highlighting three crucial aspects: Basic Math Principles, Importance of Accurate Conversion, and Common Mistakes to Avoid. By grasping these elements, individuals can ensure precision and accuracy in their calculations. The Basic Math Principles section will explore the foundational arithmetic operations that govern doubling, providing a clear understanding of how to apply these principles in practical scenarios. The Importance of Accurate Conversion will emphasize the critical role of precise unit conversions in maintaining measurement integrity. Finally, Common Mistakes to Avoid will identify frequent errors and offer strategies for mitigating them. By mastering these concepts, readers will be well-equipped to handle a wide range of measurement challenges with confidence. Let's begin by examining the Basic Math Principles that form the backbone of doubling measurements.

Basic Math Principles

Understanding the concept of doubling a measurement is rooted in basic math principles that are essential for everyday calculations, particularly in cooking and other practical applications. At its core, doubling involves multiplying a quantity by two, which can be applied to various units such as cups, grams, or inches. To grasp this concept fully, one must first understand the fundamental operations of multiplication and the concept of equivalence. Multiplication is a form of repeated addition where you add a number a certain number of times equal to another number. For example, doubling 1/3 cup means you are essentially adding 1/3 cup to itself once. Mathematically, this can be represented as \( \frac{1}{3} + \frac{1}{3} = \frac{2}{3} \). This operation relies on the principle of distributive property and the concept of fractions. Fractions are a way to represent parts of a whole and are crucial in understanding measurements. A fraction consists of a numerator (the top number) and a denominator (the bottom number), indicating how many equal parts the whole is divided into and which part you are considering. When doubling fractions, you multiply both the numerator and the denominator by two, but since you're only doubling the numerator in this case, it simplifies to adding the fraction to itself. In practical terms, if you need to double 1/3 cup of an ingredient for a recipe, you would use \( \frac{2}{3} \) cup instead. This principle extends beyond cooking; it applies to any scenario where quantities need to be scaled up or down proportionally. Moreover, understanding doubling helps in scaling recipes up or down efficiently. For instance, if a recipe serves four people and you need to serve eight, doubling all ingredients ensures that each serving remains consistent in terms of proportions. This scalability is a direct application of basic math principles like multiplication and fractions. In conclusion, doubling measurements is not just about multiplying by two; it involves a deeper understanding of mathematical operations such as addition and multiplication within the context of fractions. By mastering these basic principles, individuals can confidently adjust quantities in various contexts with precision and accuracy. Whether you're cooking for a larger group or adjusting quantities for different recipes, the ability to double measurements accurately is an invaluable skill that enhances your problem-solving abilities in everyday life.

Importance of Accurate Conversion

Accurate conversion is a cornerstone in various aspects of life, particularly when dealing with measurements. In the context of cooking, understanding how to double a measurement, such as doubling 1/3 cup, is crucial for achieving the desired outcome. The importance of accurate conversion cannot be overstated; it ensures that recipes are executed correctly, maintaining the balance of flavors and textures that define a dish. When doubling a measurement, precision is key. A slight miscalculation can lead to significant differences in the final product. For instance, if you are doubling a recipe that requires 1/3 cup of an ingredient, you must accurately convert this to 2/3 cup to avoid altering the recipe's chemistry. This precision extends beyond cooking; in fields like engineering, medicine, and science, accurate conversions are essential for safety and efficacy. In cooking, the consequences of inaccurate conversions can be immediate and noticeable. Too much or too little of an ingredient can make a dish unpalatable or even inedible. For example, doubling a recipe that includes baking powder or salt requires careful attention to ensure that the proportions remain correct. Incorrect conversions can result in baked goods that are either too dense or too salty. Moreover, accurate conversion fosters consistency and reliability. When recipes are scaled up or down, maintaining the exact proportions ensures that the final product tastes and looks as intended. This consistency is particularly important in professional kitchens where dishes must meet high standards of quality and presentation. Beyond the practical applications, understanding accurate conversion also enhances one's analytical skills. It involves a deep comprehension of fractions, ratios, and proportions—skills that are transferable across various disciplines. By mastering these concepts, individuals develop a stronger foundation in problem-solving and critical thinking. In addition to these benefits, accurate conversion promotes efficiency. When measurements are precise, there is less room for error, which means fewer wasted ingredients and less time spent on trial and error. This efficiency is especially valuable in high-pressure environments such as commercial kitchens or laboratories where time and resources are limited. Finally, the importance of accurate conversion extends to the realm of safety. In certain contexts, such as pharmaceuticals or chemical engineering, incorrect conversions can have serious consequences. Ensuring that measurements are accurate helps prevent accidents and ensures that products are safe for use. In conclusion, accurate conversion is not just a technical skill but a fundamental principle that underpins many areas of life. Whether you are doubling a recipe or working on a complex scientific project, the ability to convert measurements accurately is indispensable. It ensures quality, consistency, efficiency, and safety—making it an essential tool for anyone who values precision and reliability.

Common Mistakes to Avoid

When doubling a measurement, it is crucial to avoid common mistakes that can significantly impact the outcome of your recipe or project. One of the most frequent errors is misunderstanding the concept of doubling itself. Doubling a measurement means multiplying the original quantity by two, not just adding another unit of the same measurement. For instance, if a recipe calls for 1/3 cup of an ingredient and you need to double it, you should calculate 1/3 cup * 2, which equals 2/3 cup, not 1 cup. Another mistake is failing to consider the context in which the measurement is being used. In baking, for example, doubling ingredients can affect the chemical balance and texture of the final product. This might require adjustments in other ingredients or cooking times to maintain consistency. Additionally, when working with fractions, it's easy to misinterpret them. For example, doubling 3/4 teaspoon does not mean adding another 3/4 teaspoon; instead, you should calculate (3/4) * 2 = 1 1/2 teaspoons. Precision is key when doubling measurements. Rounding off or approximating can lead to significant discrepancies, especially in recipes where small variations can alter the final result. Always use exact measurements and avoid shortcuts that might seem convenient but could compromise accuracy. Furthermore, it's important to ensure that all ingredients are doubled proportionally. If a recipe includes multiple components with different measurements, each component must be doubled correctly to maintain the intended ratio. This is particularly important in recipes that rely on specific balances of ingredients for their success. Lastly, double-check your calculations before proceeding with your recipe or project. A simple arithmetic error can have far-reaching consequences, making it essential to verify your work. Using tools like calculators or conversion charts can help minimize mistakes and ensure that your doubled measurements are accurate. By being mindful of these common pitfalls and taking the time to accurately double your measurements, you can ensure that your recipes turn out as intended and avoid unnecessary complications. Understanding these principles will not only enhance your culinary skills but also apply broadly across various fields where precise measurement is critical.

Calculating 1/3 Cup Doubled

When it comes to measuring ingredients in cooking and baking, precision is key. One common challenge many face is calculating fractions of cups, such as doubling 1/3 cup. This article delves into the intricacies of this calculation, providing a comprehensive guide to help you master this essential skill. We will explore the **Step-by-Step Calculation Process**, breaking down the math into manageable steps to ensure accuracy. Additionally, we will discuss **Using Fractions and Equivalents**, highlighting how understanding these concepts can simplify your calculations. Finally, we will examine **Real-World Applications**, illustrating how these skills are crucial in everyday cooking and baking scenarios. By the end of this article, you will be well-equipped to handle even the most complex fraction conversions with ease. Let's begin by diving into the **Step-by-Step Calculation Process**, where we will walk through the exact steps to double 1/3 cup accurately.

Step-by-Step Calculation Process

When calculating 1/3 cup doubled, it is crucial to follow a step-by-step process to ensure accuracy and clarity. Here’s a detailed breakdown of how to achieve this calculation: 1. **Understand the Measurement**: First, recognize that 1/3 cup is a fraction of a cup. In cooking and baking, precise measurements are vital, so it's important to handle fractions carefully. 2. **Convert to Decimal Form**: To simplify calculations, convert the fraction 1/3 into its decimal equivalent. The decimal form of 1/3 is approximately 0.3333. This conversion helps in easier multiplication. 3. **Double the Measurement**: To double 1/3 cup, you need to multiply it by 2. Using the decimal form, multiply 0.3333 by 2. This gives you 0.6666. 4. **Convert Back to Fractional Form**: If you prefer working with fractions, convert the decimal back to its fractional form. The decimal 0.6666 is approximately equal to 2/3 when rounded. 5. **Verify Units**: Ensure that your final measurement is in the correct units. Since you started with cups, your doubled measurement should also be in cups. 6. **Practical Application**: In practical terms, if a recipe calls for doubling 1/3 cup of an ingredient, you would use approximately 2/3 cup of that ingredient. By following these steps meticulously—converting fractions to decimals for ease of calculation, performing the multiplication accurately, and converting back to fractions if necessary—you can confidently determine that doubling 1/3 cup results in approximately 2/3 cup. This method ensures precision and helps avoid common errors in recipe scaling, making it an essential skill for any cook or baker.

Using Fractions and Equivalents

When calculating measurements, especially in cooking and baking, understanding fractions and their equivalents is crucial for accuracy. The concept of doubling a fraction, such as doubling 1/3 cup, hinges on this foundational knowledge. To begin with, fractions represent parts of a whole, where the numerator indicates the number of parts and the denominator specifies the total number of parts that make up the whole. For instance, 1/3 means one out of three equal parts. To double 1/3 cup, you need to multiply both the numerator and the denominator by two. This process involves basic arithmetic operations but requires a clear grasp of fraction multiplication. When you multiply 1/3 by 2, you are essentially finding two times one-third. Mathematically, this is expressed as \( \frac{1}{3} \times 2 = \frac{2}{3} \). Therefore, doubling 1/3 cup results in \( \frac{2}{3} \) cup. Understanding equivalents is also vital in this context. Equivalents allow you to convert between different units or forms of measurement seamlessly. For example, knowing that 1 cup is equal to 8 ounces or 16 tablespoons can be very helpful when scaling recipes. If a recipe calls for doubling an ingredient measured in cups but you only have a measuring spoon or scale, being able to convert between these units ensures precision. In practical terms, if you need to measure out \( \frac{2}{3} \) cup using common kitchen tools, you can use the equivalent measurements. Since 1 cup equals 8 ounces or 16 tablespoons, \( \frac{2}{3} \) cup would be approximately 5.33 ounces or about 10.67 tablespoons. This conversion helps in scenarios where precise cup measurements are not available or when working with ingredients that are easier to measure in other units. Moreover, recognizing that fractions can be simplified or converted into decimals enhances flexibility in calculations. For instance, \( \frac{2}{3} \) can be converted into a decimal by dividing the numerator by the denominator: \( \frac{2}{3} = 0.6667 \). This decimal form can be particularly useful when using digital scales or when precision is paramount. In summary, mastering fractions and their equivalents is essential for accurate measurement conversions in cooking and baking. Doubling 1/3 cup to get \( \frac{2}{3} \) cup involves straightforward fraction multiplication and understanding how these measurements translate across different units. By leveraging these mathematical concepts and conversion tools, cooks and bakers can ensure that their recipes are scaled correctly and consistently yield desired results. This foundational knowledge not only simplifies the process but also fosters confidence in the kitchen, allowing for more creative experimentation and reliable outcomes.

Real-World Applications

In the realm of everyday life, understanding measurements like calculating 1/3 cup doubled is more than just a mathematical exercise; it has numerous real-world applications that make cooking, baking, and even scientific experiments more precise and efficient. For instance, in the kitchen, doubling a recipe can be crucial for hosting larger gatherings or preparing meals in bulk. Knowing that 1/3 cup doubled equals 2/3 cup ensures that ingredients are proportionally adjusted, maintaining the balance of flavors and textures that define a dish. This precision is particularly important in baking, where small variations can significantly impact the final product's quality. Beyond culinary arts, in scientific research and laboratory settings, accurate measurements are paramount. Scientists often need to scale up experiments from small pilot studies to larger trials, and understanding how to double or triple quantities without compromising the integrity of the experiment is essential. For example, in chemistry, doubling a solution's volume while maintaining its concentration requires precise calculations to avoid errors that could skew results. Additionally, in agriculture and horticulture, farmers may need to adjust fertilizer or pesticide applications based on the size of their plots, and accurate scaling ensures optimal use of resources without over- or under-treating the land. In healthcare, pharmacists must accurately scale drug dosages for patients, and understanding how to double or halve quantities is critical for patient safety. Even in DIY projects and home improvement tasks, such as mixing paints or preparing concrete, knowing how to adjust ingredient ratios ensures that the final product meets desired specifications. Thus, the ability to calculate measurements like 1/3 cup doubled is not just a trivial skill but a fundamental tool that enhances accuracy and efficiency across various domains, making it an indispensable part of our daily lives.

Practical Applications and Examples

In the realm of practical applications, understanding the nuances of measurement and conversion is crucial for achieving precision and excellence. This article delves into three pivotal areas that highlight the importance of meticulous measurement: Cooking and Baking Scenarios, Converting Between Units, and Tips for Precision in Recipes. Each of these sections offers valuable insights into how accurate measurements can transform everyday tasks into masterful executions. For instance, in cooking and baking, the difference between a pinch of salt and a dash of sugar can be the deciding factor between a dish that is merely good and one that is exceptional. Converting between units seamlessly ensures that recipes are executed correctly, regardless of the measurement system used. Additionally, tips for precision in recipes provide essential guidelines for minimizing errors and maximizing flavor. By exploring these practical applications, readers will gain a deeper understanding of how precise measurements can elevate their culinary skills. Let's begin by examining the critical role of accurate measurements in Cooking and Baking Scenarios.

Cooking and Baking Scenarios

In the realm of cooking and baking, understanding measurements is crucial for achieving consistent and delicious results. One common query that arises, especially for novice bakers, is how to double a recipe, specifically when dealing with fractions like 1/3 cup. To illustrate this, let's delve into practical applications and examples that highlight the importance of accurate measurement doubling. When doubling a recipe, it's essential to understand that each ingredient must be multiplied by two. For instance, if a recipe calls for 1/3 cup of sugar and you want to double it, you need to calculate what 2/3 cup is. This can be done by simply multiplying the fraction by two: \( \frac{1}{3} \times 2 = \frac{2}{3} \) cup. This straightforward calculation ensures that your doubled recipe maintains the original balance of flavors and textures. Consider a scenario where you're baking a batch of cookies that requires 1/3 cup of butter. If you decide to double the recipe to make more cookies, you'll need \( \frac{2}{3} \) cup of butter. Similarly, if a cake recipe calls for 1/3 cup of milk and you're doubling it, you'll need \( \frac{2}{3} \) cup of milk. These precise measurements are vital because even small discrepancies can affect the final product's consistency and taste. Another practical example involves making a double batch of homemade granola. If the original recipe requires 1/3 cup of honey, doubling it would mean using \( \frac{2}{3} \) cup of honey. This ensures that the granola has the right amount of sweetness without becoming overly sticky or dry. Moreover, understanding how to double fractions helps in scaling recipes up or down efficiently. For instance, if you're hosting a large gathering and need to triple or quadruple a recipe, knowing how to handle fractions like 1/3 cup becomes indispensable. By multiplying the fraction by the desired factor (e.g., \( \frac{1}{3} \times 3 = 1 \) cup for tripling), you can confidently adjust ingredient quantities without compromising on quality. In summary, mastering the art of doubling fractions in cooking and baking is a fundamental skill that enhances your culinary repertoire. Whether you're making cookies, cakes, granola, or any other dish, accurately doubling ingredients like 1/3 cup ensures that your creations turn out as intended—delicious and consistent every time. This precision not only saves time but also builds confidence in the kitchen, allowing you to experiment with new recipes and variations with ease.

Converting Between Units

Converting between units is a fundamental skill that underpins various practical applications in everyday life, from cooking and baking to science and engineering. This process involves changing the measurement of a quantity from one unit to another, ensuring accuracy and consistency across different contexts. For instance, in cooking, converting between units can be crucial for achieving the right proportions of ingredients. Consider the question "what is 1/3 cup doubled?" To answer this, you need to understand how to convert fractions and volumes. In this case, doubling 1/3 cup means multiplying it by two. Since 1/3 cup is equivalent to approximately 2.67 fluid ounces or about 79.25 milliliters, doubling these values gives you 5.33 fluid ounces or 158.5 milliliters. This conversion is essential for scaling recipes up or down without compromising the final product's quality. Beyond cooking, unit conversions are vital in scientific research and engineering. For example, converting between metric and imperial units can be necessary when working with data from different sources. In physics, converting between units of length, mass, and time is critical for calculations involving velocity, acceleration, and force. The ability to convert units accurately ensures that measurements are consistent and reliable, which is paramount for drawing accurate conclusions and making informed decisions. In real-world scenarios, such as construction or manufacturing, precise unit conversions can mean the difference between success and failure. For instance, converting between feet and meters or pounds and kilograms can affect the structural integrity of a building or the performance of a machine. Misconversions can lead to costly errors and safety hazards. Moreover, technology has made unit conversions more accessible than ever. Online conversion tools and calculators can quickly convert between various units, saving time and reducing the likelihood of human error. However, understanding the underlying principles of unit conversion remains essential for verifying results and ensuring that calculations are correct. In summary, converting between units is an indispensable skill with numerous practical applications across different fields. Whether you are a chef scaling a recipe, a scientist analyzing data, or an engineer designing a new product, the ability to accurately convert units is crucial for achieving precise results and avoiding potential pitfalls. By mastering this skill, individuals can enhance their efficiency, accuracy, and overall performance in their respective domains.

Tips for Precision in Recipes

When it comes to precision in recipes, even the smallest miscalculation can significantly impact the final outcome. Here are some tips to ensure accuracy and consistency in your culinary endeavors. First, **measure ingredients carefully**: Use digital scales for dry ingredients and measuring cups for liquids. When measuring dry ingredients like flour, spoon them into the measuring cup rather than scooping directly from the container to avoid compacting the ingredient. For liquids, place the measuring cup on a flat surface and read the measurement at eye level to avoid errors. **Understand unit conversions**: Familiarize yourself with common conversions such as teaspoons to tablespoons (1 tablespoon = 3 teaspoons) and cups to milliliters (1 cup = approximately 236.6 milliliters). This knowledge is crucial when scaling recipes up or down. For instance, if a recipe calls for 1/3 cup of an ingredient and you need to double it, you would need 2/3 cup. **Follow the sequence of operations**: Recipes often list ingredients in the order they are used. Adhering to this sequence helps ensure that each component is incorporated correctly. This is particularly important in baking where chemical reactions between ingredients can be sensitive to timing and order. **Use the right tools**: Invest in quality kitchen tools such as silicone spatulas, stainless steel measuring spoons, and non-stick pans. These tools not only make cooking easier but also help maintain precision by providing accurate measurements and even heat distribution. **Read recipes thoroughly**: Before starting to cook, read through the entire recipe at least once. This helps you understand what is required and allows you to prepare all necessary ingredients and tools beforehand. It also alerts you to any special instructions or techniques that might be critical for success. **Practice makes perfect**: The more you cook, the more comfortable you become with measuring ingredients accurately and following recipes precisely. Start with simple recipes and gradually move on to more complex ones as your confidence grows. In practical applications, these tips are invaluable. For example, when doubling a recipe that calls for 1/3 cup of sugar, you would need exactly 2/3 cup of sugar to maintain the balance of flavors and textures. This precision ensures that your dish turns out as intended without any unexpected variations. By incorporating these tips into your cooking routine, you enhance your ability to replicate recipes consistently and confidently. Whether you're a novice cook or an experienced chef, attention to detail in measuring ingredients and following instructions is key to achieving culinary excellence.