Understanding the Concept of Inflection Points

The Definition of Inflection Points

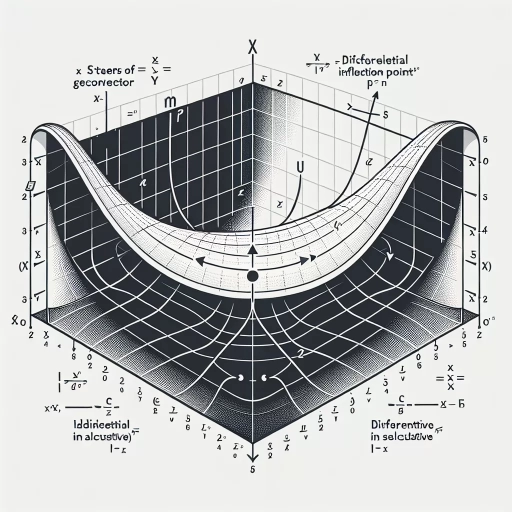
An inflection point, in the realm of calculus, is a point on a plane curve at which the curve switches from being concave upward to concave downward, or vice-versa. Identified by the curvature, an inflection point is a point where the curve changes its bending direction. Understanding the concept of inflection points is crucial for solving complex calculus problems, interpreting graphs, and in the study of various scientific fields like physics and engineering.

The Mathematical Representation of Inflection Points

Mathematically, an inflection point exists at `(x,y)` if the function `f(x)` is continuous at `(x,y)`, and the function's second derivative `f''(x)` either changes its sign at `x` or equals zero and changes its sign somewhere around `x`. This mathematical representation further solidifies the understanding of the concept at a numerical level, making it easier to spot inflection points on a graph or in a function.

Applications of Inflection Points

Inflection points have widespread applications beyond just the academic viewpoint. In business and economics, an inflection point can signal a significant event in a company or market's behavior. Further, curvatures and inflection points are key in computer graphics to develop curve design algorithms that provide a more realistic representation. This makes the comprehension of inflection points practical and applicable in real-world scenarios.

Techniques to Determine Inflection Points

Using the Second Derivative Test

The second derivative test is the most famous method to determine the inflection point. If the original function is twice differentiable, then an inflection point occurs exactly where the second derivative is equal to zero, and the sign changes on either side of the point. This method reduces the problem to a simpler algebraic process, making it an efficient and straightforward way for finding inflection points.

Graphical Representation

Another approach to spot inflection points is through graphical representation. When graphed, an inflection point is usually distinguished as a point on the function where the graph changes concavity. This means that the graph switches between bending upwards and downwards at the inflection point, which can be visually discerned.

Utilizing Inflection Point Figure Algorithms

Advanced learners or individuals dealing with complex functions and curves may also opt to utilize inflection point figure algorithms, which are mathematical algorithms designed to automate the process of spoting inflection points. These sophisticated tools are commonly utilized in computer graphics and advanced mathematical studies.

Common Mistakes to Avoid When Finding Inflection Points

Confusing Inflection Points with Turning Points

One common mistake is confusing inflection points with turning points. While they can sometimes coincide, a turning point represents a local maximum or minimum on a graph, while an inflection point is where the curve changes its concavity. Therefore, it is crucial to understand the distinctive characteristics of each to not interchange them unintentionally.

Overlooking the Continuity of a Function

Frequently, learners overlook that for an inflection point to exist, the function must be continuous at that point. This means it cannot have breaks, jumps, or holes. If the function is not continuous, even if the second derivative equals zero, it cannot be considered an inflection point.

Neglecting the Sign Change

Another common mistake is neglecting the critical sign change. A change in the curvature of a graph means a change from positive to negative concavity or vice versa. Even if the second derivative equals zero at some point, it must be paired with a different sign on both sides of the point to be considered an inflection point.